2.8. Tutorial Exercises: non-parametric tests

Here are some exercises on comparing groups of data (medians or means) using rank-based non-parametric tests, or permutation tests

2.8.1. Set up Python libraries

As usual, run the code cell below to import the relevant Python libraries

# Set-up Python libraries - you need to run this but you don't need to change it
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pandas as pd
import seaborn as sns
sns.set_theme(style='white')
import statsmodels.api as sm
import statsmodels.formula.api as smf
import warnings 
warnings.simplefilter('ignore', category=FutureWarning)

2.8.2. 1. Whose peaches are heavier?

Mr Robinson’s juice factory buys peaches from farmers by the tray. Each tray contains 50 peaches. Farmer McDonald claims that this is unfair as his peaches are juicier and therefore weigh more than the peaches of his rival, Mr McGregor.

Mr Robinson weighs eight trays of Farmer McDonald’s peaches and 8 trays of Mr McGregor’s peaches.

Investigate whether McDonald’s claim is justified by testing for a difference in weight between McDonald and McGregor’s peaches using a non-parametric (rank-based) test.

a) Load the data into a Pandas dataframe

peaches = pd.read_csv('https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/data/peaches.csv')
peaches

	McGregor	MacDonald
0	7.867	8.289
1	7.637	7.972
2	7.652	8.237
3	7.772	7.789
4	7.510	7.345
5	7.743	7.861
6	7.356	7.779
7	7.944	7.974

b) Plot the data and comment.

A Kernel desity estimate plot (to show the distribution) and rug plot (to show individual data points) would be a good choice here. You should comment on the data distribution

# your code here to plot the data

c) Conduct an appropriate rank-based non-parametric test of Farmer McDonald’s claim

• State your hypotheses

• State relevant descriptive statistics

• Carry out the test using the built in function from scipy.stats with appropriate option choices

• State your conclusions

# your code here

d) Conduct a permutation test of the same claim

• State your hypotheses

• State relevant descriptive statistics

• Carry out the test using the built in function from scipy.stats with appropriate option choices

• State your conclusions

# your code here

2.8.3. 2. IQ and vitamins

The VitalVit company claim that after taking their VitalVit supplement, IQ is increased.

They run a trial in which 22 participants complete a baseline IQ test, then take VitalVit for six weeks, then complete another IQ test.

a) What kind of design is this.

< your answer here >

b) What are the advantages and possible disadvantages of this type of design? Should the company have done something different or additional to rule out confounding factors?

< your answer here >

c) Load the data into a Pandas dataframe

vitamin = pd.read_csv('https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/data/vitalVit.csv')
vitamin

	ID_code	before	after
0	688870	82.596	83.437
1	723650	117.200	119.810
2	445960	85.861	83.976
3	708780	125.640	127.680
4	109960	96.751	99.103
5	968530	105.680	106.890
6	164930	142.410	145.550
7	744410	109.650	109.320
8	499380	128.210	125.110
9	290560	84.773	87.249
10	780690	110.470	112.650
11	660820	100.870	99.074
12	758780	94.117	95.951
13	363320	96.952	96.801
14	638840	86.280	87.669
15	483930	89.413	94.379
16	102800	85.283	88.316
17	581620	94.477	96.300
18	754980	90.649	94.158
19	268960	103.190	104.300
20	314040	92.880	94.556
21	324960	97.843	97.969

d) Plot the data and comment. A scatterplot would be a good choice as these are paired data. You could add the line of equality (line x=y) to the graph so we can see whether most people score higer on the IQ test before or after taking VitalVit

# Your code here for a scatter plot.

e) Conduct a suitable rank-based non-parametric test of VitalVit’s claim

• State your hypotheses

• State relevant descriptive statistics

• Carry out the test using the built in function from scipy.stats with appropriate option choices

• State your conclusions

# your code here

f) Conduct a suitable permutation test of VitalVit’s claim

• State your hypotheses

• State relevant descriptive statistics

• Carry out the test using the built in function from scipy.stats with appropriate option choices

• State your conclusions

# your code here

2.8.4. 3. Socks

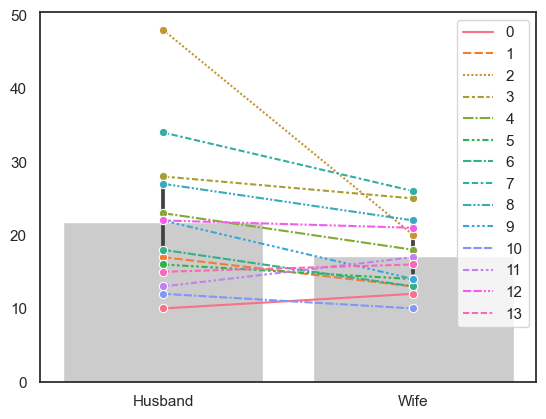
In the section on permutation testing, we introduced a dataset on sock ownership (number of pairs of socks owned for 14 husband-wife couples. We noticed that when using a permutation test for difference of means, the null distribution of the difference of means was strongly affected by the presences of an outlier:

• in one couple the husband owned about 30 more pairs of socks than the wife

• wheter the difference of means in each permutation was positive or negative depended disproportionately on whether this couple were ‘flipped’ or not in that particular permutation

Let’s compare the use of the rank-based (Wilcoxon’s Sign-Rank test) test with the permutation test for the mean difference.

a. Load the data (done for you)

socks = pd.read_csv('https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/data/socks.csv')
socks

	Husband	Wife
0	10	12
1	17	13
2	48	20
3	28	25
4	23	18
5	16	14
6	18	13
7	34	26
8	27	22
9	22	14
10	12	10
11	13	17
12	22	21
13	15	16

b. Plot the data (done for you)

sns.barplot(data=socks, color=[0.8,0.8,0.8])
sns.lineplot(data=socks.T, marker='o')
plt.show()

c. Carry out a suitable rank-based non-parametric test of the hypothesis that men own more socks than women

# your code here

d. Carry out a suitable permutation test test of the hypothesis that men own more socks than women

# your code here

e. Compare the two tests.

In this case the rank-based test has a (slightly) smaller \(p\)-value than the permutation test.

The permutation test preserves thhe following features of the data:

1. In each couple one partner usually has more socks (what we shuffle is which partner this is)

2. One couple has an extreme difference in sock-counts (we shuffle whether it is the husband or wife who has more socks)

3. We retain the sample sizes and overall distribution of difference of means

The rank-based test ‘neutralizes’ one of these features, which is it and what is the effect?