2D Data: Correlation and Pairwise Effects

2.6. 2D Data: Correlation and Pairwise Effects#

In some datasets, the key point of interest is the relationship between two variables. Important experimental examples would be:

paried designs (where pairs of participants are compared, to balance out external variables) - for example:
- patients and control participants may be matched on age and sex
Repeated measures designs, where the same participant completes all conditions in the experiment
- A patient’s blood pressure before and after taking a drug
- Reaction time on the same task with and without distraction

Here is a video about paired vs unpaired designs:

%%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/yq5RF2MCN7Y?si=1XDbQKpZP-KYSoWG" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe>

If we want to see the relationship between paired measurements, we need a type of plot that shows that relationship. Good examples are:

scatterplot sns.scatterplot()
scatterplot with regression line sns.regplot()
2D histogram sns.histplot()
2D KDE plot sns.kde()

Here is a video about plotting paired measurements:

%%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/lVHzI2Ktd_s?si=_112tUvkxO9ESikm" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe>

2.6.1. Example: brother/sister heights#

A picture of people of different heights

A researcher hypothesises that men are taller than women.

He also notices that there is a considerable genetic influence on height, with some families being taller than others

He decides to control for this by comparing the heights of brothers and sisters (shared genetic influence, shared upbringing). This is a paired design.

I have provided some made-up data

Note that datasets with multiple measurements for each individual tend to be presented as wideform tables - that is, with one row per ‘case’ (person, family etc) and one column per variable measured - the plotting examples below therefore use wideform data.

A solution for longform data is covered briefly at the end of this notebook

Set up Python libraries#

As usual, run the code cell below to import the relevant Python libraries

# Set-up Python libraries - you need to run this but you don't need to change it
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pandas as pd
import seaborn as sns
sns.set_theme(style='white')
import statsmodels.api as sm
import statsmodels.formula.api as smf
import warnings
warnings.simplefilter('ignore', category=FutureWarning)

Load and inspect the data#

Load the file BrotherSisterData.csv which contains heights in cm for 25 fictional brother-sister pairs

heightData = pd.read_csv('https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/data/BrotherSisterData.csv')
display(heightData)

	brother	sister
0	174	172
1	183	180
2	154	148
3	172	180
4	172	165
5	161	159
6	167	159
7	172	164
8	195	188
9	189	175
10	161	160
11	181	177
12	175	168
13	170	169
14	175	165
15	169	164
16	169	163
17	180	176
18	180	176
19	180	172
20	175	170
21	162	157
22	175	172
23	181	179
24	173	171

Independent KDE plots#

Let’s use a KDE plot to compare the heights of the men (brothers) and women (sisters) in the sample.

We can call KDE plot twice to plot the data from brothers and sisters overlayed

sns.kdeplot(data=heightData, fill=True)
plt.xlabel('height (cm)')

Text(0.5, 0, 'height (cm)')

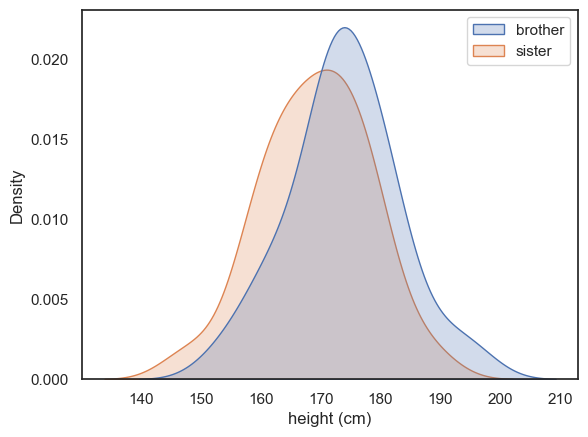
../_images/210969502b0f409e88c367c59eab5d812e47a8e08737338faea7e5a44bd2ef35.png

There’s a lot of overlap for sure, and just a hint that the men are taller than the women.

But comparing all the men to all the women is wasting the power of our paired design! We deliberated measured brother-sister pairs in the hope of “cancelling out” shared genetic or environmental influences within families. We therefore need to ask if each brother is taller than his own sister.

2.6.2. Scatterplot#

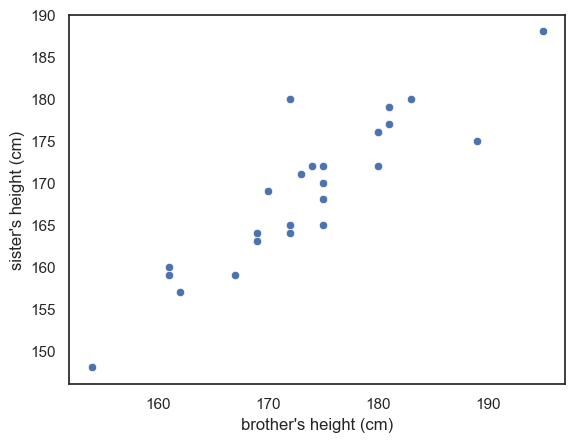
On a scatterplot, each dot represents two people - a brother and sister:

sns.scatterplot(data=heightData, x='brother', y='sister')
plt.xlabel("brother's height (cm)")
plt.ylabel("sister's height (cm)")
plt.show()

../_images/ece6f3ca7f38479d56557d7b27488a473e91b99ad3f96d4f8ec02c98b201260a.png

sns.scatterplot(data=heightData)
plt.xlabel("brother's height (cm)")
plt.ylabel("sister's height (cm)")
plt.show()

../_images/5a2eda28977be3b8713de68eecaaa18bb6d613eff465f52e64ff4b2f4355f824.png

Between-pairs effect (correlation)#

Notice that in the scatterplot, the data points are spread out along a diagonal line, or to put it another way, height of brothers and sisters is correlated across families.

This means that in general tall brothers have tall sisters and this variation between families rather dwarfs the effect of interest (that within each family the brother is taller than his own sister)

This feature of the plot is evidence that a paired design was a particularly good choice for this question - in the paired design, the (large) variation between families is cancelled out allowing us to detect the (small) difference between male and females.

Within-pairs effect (pairwise difference)#

The family effect is actually “noise” in this study - what we really want to know is not whether some families are taller than others, but whether the male sibling in each family is taller than the female sibling once the family effect is accounted for (by compaaring only within families).

To help us visualise this we add a reference line.

Reference line#

If all the brothers were exactly the same height as their sisters, we would expect all data points to fall exactly on the line \(x=y\)

If brothers were roughly the same height as their sisters (with some random variation) we would expect the data points to fall equally often above and below the line \(x=y\)

If brothers are generally taller than their sisters, most of the datapoints will fall on one side of the line (think about which!)

To add the line \(x=y\) we use the matplotlib function plt.plot(). The arguments of this function are the \(x\) and \(y\) values for the ends of the line (\(x\) and \(y\) both range from 150-190), and the argument ‘r–’ which sets the color and line type.

sns.scatterplot(data=heightData, x='brother', y='sister')
plt.xlabel("brother's height (cm)")
plt.ylabel("sister's height (cm)")
plt.plot([150, 190],[150, 190], 'r--')
plt.show()

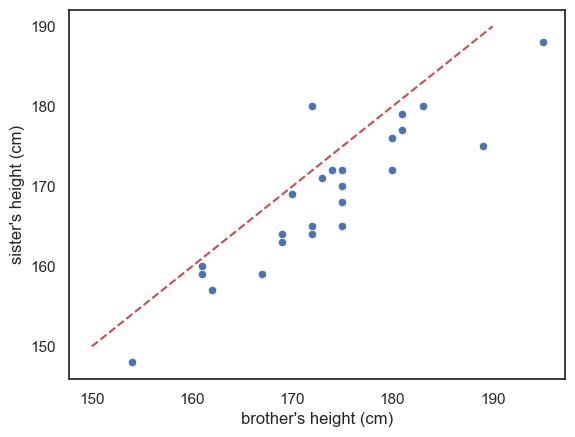
../_images/7974f010c5557a69dbcd3313905ce333e58ead4a4bab159a939bba665a9def2b.png

Look at the graph - most of the datapoints fall on one side of the line (below it)

This means either than most of the brothers are taller than their sisters, or vice versa - which is it (look at the graph)?

Exercise#

See if you can add another line of code to draw a red horizontal line at y=170

Reference line is not a regression line#

More commonly, when you see a line on a scatter plot, the line is a regression line (more detail below). It can be helpful to add other reference lines, such as the line \(x=y\), but I suggest you use obvious colouring (eg a red dashed line) to distinguish them from a regression line, and clearly state in the figure description (ie the text under the figure) that the red dashed line is the line \(x=y\) for reference

2.6.3. Scatterplot with regression line#

Sometimes we are interested in the between-pairs effect. For example we might be interested in the shared effect of genetics/environment, and would like to make a prediction along the lines ‘for each additional cm in height of the brother, we expect the height of his sister to increase by 0.8cm’

We will cover regression analysis later in the course

Here I just want to introduce a version of the scatterplot which includes the best fitting regression line, sns.regplot()

sns.regplot(data=heightData, x='brother', y='sister')
plt.plot([150, 190],[150, 190], 'r--')
plt.xlabel("brother's height (cm)")
plt.ylabel("sister's height (cm)")
plt.show()

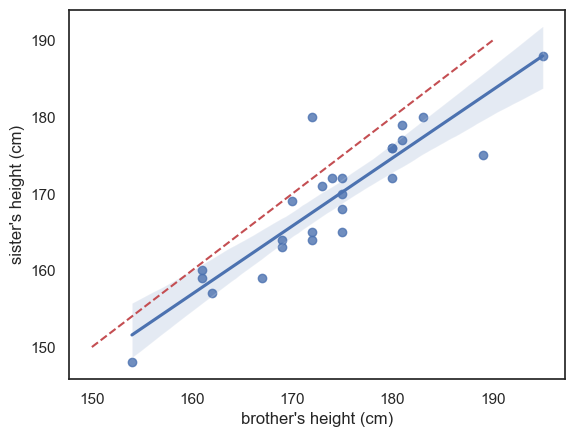
../_images/0878d651cb2f1f917655241bc8faa7b966088809d1be477dd596a2060d4a0883.png

The blue line is the regression line (and the shading represents a confidence interval for the regression line - we will cover confidence intervals in detail later but basically, it reflects the fact that we are not totally sure this sample reflects all men and women in the popluation; we expect the ‘true’ regression line to fall somewhere in the shaded region)

I’ve also included (red dashed line) the line \(x=y\) for reference - we can see that the regression line is not the same as the line \(x=y\) - it falls to one side of \(x=y\) and has a slightly different slope.

If these ideas (regression line and confidence interval) are unfamiliar please think no more about it - they will be covered later in the course, but I mention this plot here so you have all commonly used plots in one chapter for revision.

2.6.4. Jointplot#

A disadvantage of the scatterplot is that we lose the ability to see the shape of each distribution (brothers’ and sisters’ heights), which we would get from a histogram or KDE plot

is the distribution of heights symmetrical or skewed?
is the distribution unimodal or bimodal

We can get ‘the best of both worlds’ by using seaborn function jointplot, which shows the marginal distributions (the height distributions for brothers and sisters separately) at the side of the main scatter plot

sns.jointplot(data=heightData, x='brother', y='sister')
plt.xlabel("brother's height (cm)")
plt.ylabel("sister's height (cm)")
plt.plot()

[]

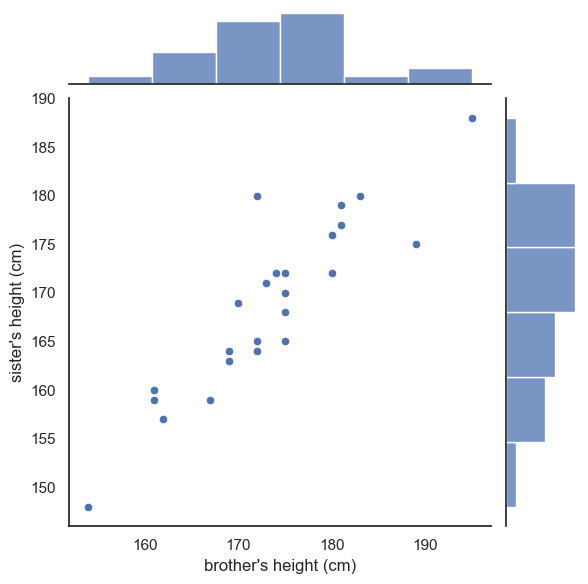
../_images/66aa3cc7c284cab8c21776087d892f0f477cb42b9c3db83f320863386ee575fd.png

Since this plot is now made up of three axes (the main scatter plot and the two marginal histograms), if we want to adjust one of those axes, we use a set of arguments in a dictionary:

marginal_kws are keyword argumments for the marginal histograms
joint_kws are keyword arguments for the scatterplot itself

You can probably just copy this syntax without worrying too much about understanding it as we don’t make heavy use of dictionaries in this course.

sns.jointplot(data=heightData, x='brother', y='sister', kind='scatter', 
              marginal_kws=dict(bins=range(150,200,5), kde="true"), 
              joint_kws=dict(color='k'))
plt.show()

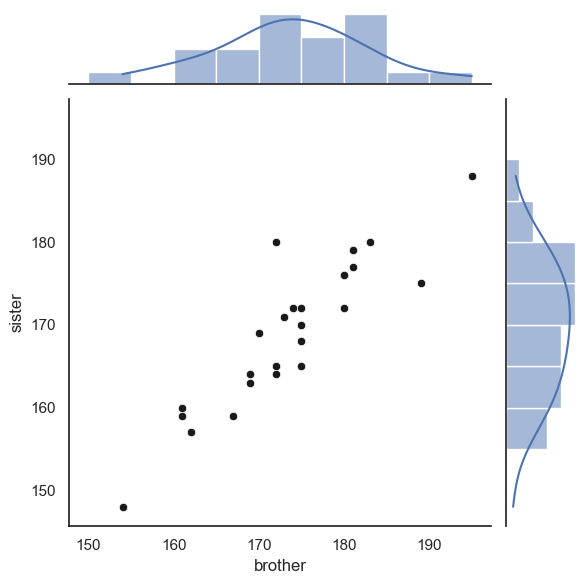
../_images/338d5882bd41df7c6dfc35d8a6e44be7c42b2a46baf9ada44e5c20589328e454.png

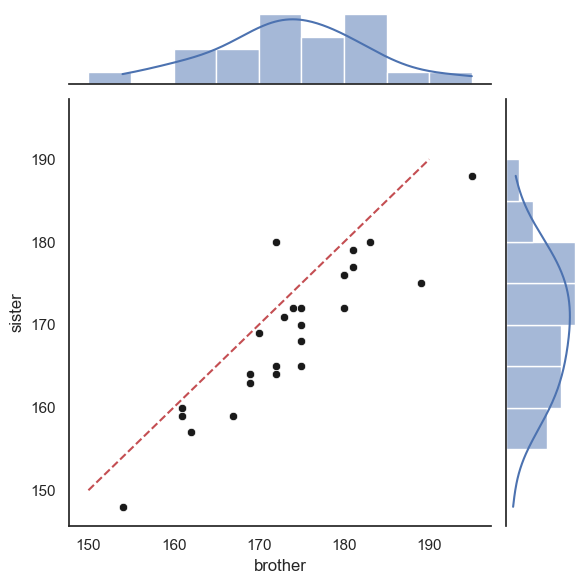
Finally, we can add the line \(x=y\).

This is a little fiddly and you will not be required to do this in an assessment - however I include it for your future reference

As the plot consists of several axes, we have to tell the computer which part of the the joint plot to add the line to, by getting a handle to the plot (see comments in the code)

# create the joint plot as before but give it a label - "myfig"
myfig = sns.jointplot(data = heightData, x='brother', y='sister', kind='scatter',
                      marginal_kws=dict(bins=range(150,200,5), kde="true"),
                      joint_kws=dict(color='k'))

# plot the line x=y onto the joint axis (ax_joint) of myfig
myfig.ax_joint.plot([150,190],[150,190],'r--')

plt.show()

../_images/d8bbe64137795269da9ae84429356352386a1aa57b19676e9e3e0209fdb19741.png

2.6.5. 2D Histogram#

The functions sns.histplot() and sns.kde() can actuaally be used for two dimensional data.

Here is a histplot for our brother-sister height data, with the scatterplot overlaid:

sns.histplot(data=heightData, x='brother', y='sister', bins=range(150,200,5))
sns.scatterplot(data=heightData, x='brother', y='sister', color='k')

plt.show()

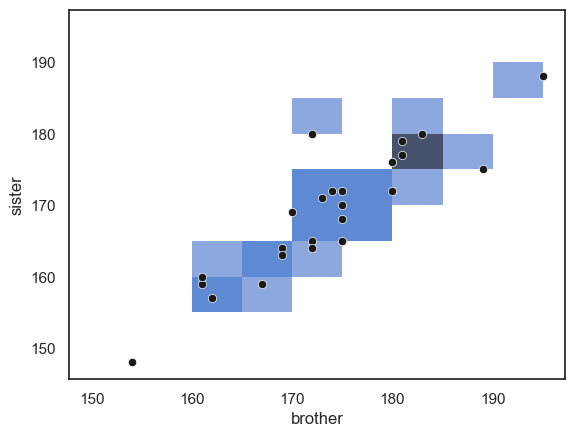
../_images/7d615c91d9405ecb9757c6928977c93d81c4515bc95450aee238188948e21b45.png

… Note that areas (squares) with more data points in them are darker blue.

Large datasets#

A 2D histogram or KDE plot is particularly useful when a dataset is too large to be successfully visualized using a scatterplot.

For example, consider the following dataset containing heights, weight and gender for 10,000 (fictional) people.

hws = pd.read_csv('https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/data/weight-height.csv')
display(hws)

	Gender	Height	Weight
0	Male	73.847017	241.893563
1	Male	68.781904	162.310473
2	Male	74.110105	212.740856
3	Male	71.730978	220.042470
4	Male	69.881796	206.349801
...	...	...	...
9995	Female	66.172652	136.777454
9996	Female	67.067155	170.867906
9997	Female	63.867992	128.475319
9998	Female	69.034243	163.852461
9999	Female	61.944246	113.649103

10000 rows × 3 columns

Let’s try making a scatterplot of the data:

sns.scatterplot(data=hws, x='Height', y='Weight')
plt.show()

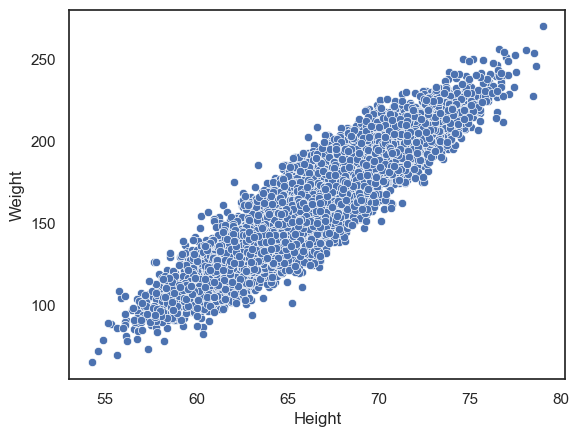
../_images/a55da70b261dde3e495dd1d7db5adb2938a1776ae4da67e0903e76b8b5885c16.png

We can clearly see a positive correlation between weight and height, but it is hard to see any detail about the relationship as the dots are packed so closely together.

We can try instead to plot a 2D histogram:

sns.histplot(data=hws, x='Height', y='Weight')
plt.show()

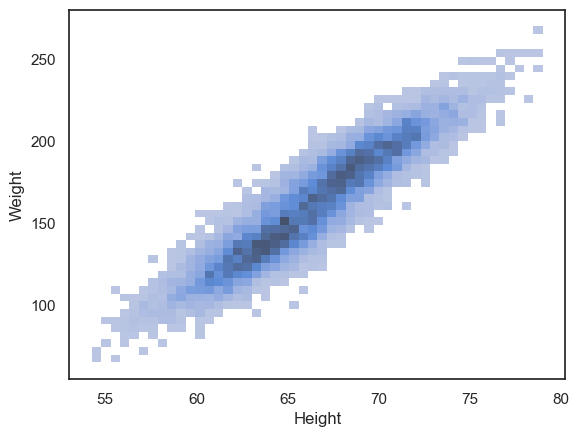
../_images/4a7c5dfa8b7bc0264dfddeb0bc167f53cfe8322203da8b4e80f6f7224d17a418.png

We can now see that the density of datapoints is higher in the middle of the cloud, and interestingly can see a hint that there are two separate peaks within the data distribution (look closely - the dark region of the histogram dips in the middle).

The reason for this becomes clearer if we plot the data separately for men and women:

sns.histplot(data=hws, x='Height', y='Weight', hue='Gender')
plt.show()

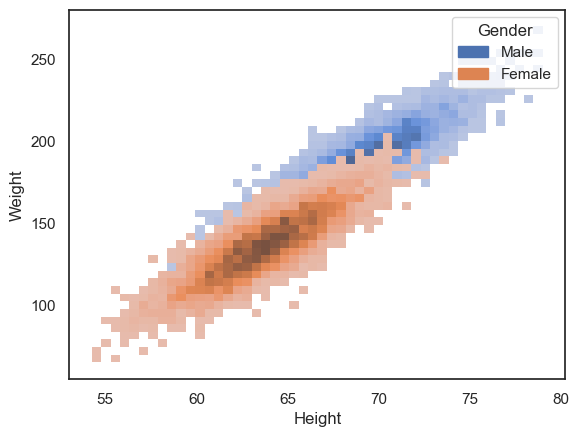
../_images/42f8a558c5580dc35d0086baeecaa7bf9ce77d59f095bf367bad00eb22bd1a3f.png

However, the data cloud for women is now occluding the data cloud for men.

Another option is to use the 2D KDE plot, which produces a kind of contour map (equivalent to the kind fo map you would take hill walking):

sns.kdeplot(data=hws, x='Height', y='Weight', hue='Gender')
plt.show()

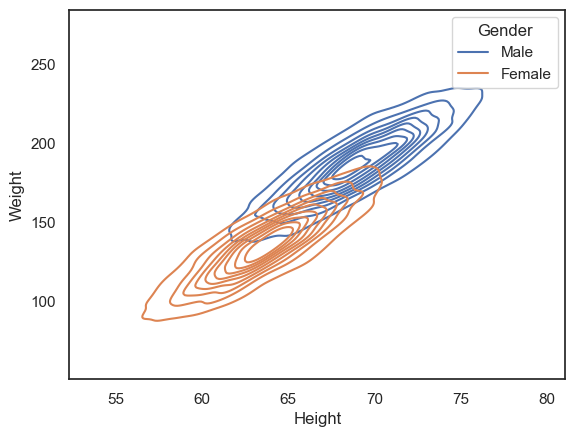
../_images/d47ad180ca55f1033e1e63c3b677fafa6eec4d139963127cb557d8062daebb7e.png

Customization#

All the plots above can be customized to highlight features of interest in the data.

Particularly relevant tweaks for these plot types are:

alpha - a number between 0 and 1 - makes plots semi-transparent when close to 0
colormap

You can learn more on the seaborn reference pages for sns.histplot(), sns.kdeplot() and sns.scatter().

2.6.6. Longform vs wideform data#

Data tables can be either longform, or wideform.

In wideform (as in the examples above), each row corresponds to one ‘case’ or ‘record’ and each column corresponds to one variable

In the two examples above we have:

records = families; variables = height of brother, height of sister
records = individuals; variables = sex, height, weight

In longform data, the grouping variables are given in a column - for example in the following longform version of the brother/sister heights data, we can tell which brother and sister belong to the same family by checking the familyID variable.

heightDataLongform = pd.read_csv('https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/data/BrotherSisterDataLongform.csv')
heightDataLongform

	familyID	sex	height
0	410119	Male	174
1	438181	Male	183
2	260033	Male	154
3	330754	Male	172
4	118173	Male	172
5	218511	Male	161
6	934515	Male	167
7	936244	Male	172
8	608784	Male	195
9	700114	Male	189
10	902900	Male	161
11	327878	Male	181
12	714099	Male	175
13	136536	Male	170
14	483548	Male	175
15	992816	Male	169
16	427440	Male	169
17	809371	Male	180
18	578843	Male	180
19	342207	Male	180
20	565176	Male	175
21	626851	Male	162
22	185965	Male	175
23	165826	Male	181
24	819334	Male	173
25	410119	Female	172
26	438181	Female	180
27	260033	Female	148
28	330754	Female	180
29	118173	Female	165
30	218511	Female	159
31	934515	Female	159
32	936244	Female	164
33	608784	Female	188
34	700114	Female	175
35	902900	Female	160
36	327878	Female	177
37	714099	Female	168
38	136536	Female	169
39	483548	Female	165
40	992816	Female	164
41	427440	Female	163
42	809371	Female	176
43	578843	Female	176
44	342207	Female	172
45	565176	Female	170
46	626851	Female	157
47	185965	Female	172
48	165826	Female	179
49	819334	Female	171

When we have multiple measurements one individual, wideform often seems more natural. Examples in which we would have multiple measurements for one individual are:

test scores before- and after- an intervention
multiple health metrics such as weight, blood pressure and pulse
responses to multiple questions in a survey
data on a single variable for paired individuals (such as height of brother/sister or husband/wife pairs)

Why would we ever use the longform format?

when the number of measurements in each ‘record’ or ‘group’ is variable (eg heights of all siblings in each family - the number of siblings will vary across families)

2.6.7. Converting longform to wideform#

To convert longform data to wideform (for use with plotting functions such as sns.scatterplot and sns.regplot) we use the pandas function df.pivot

We need to tell df.pivot which variable to group by (that is, which variable indexs the datapoints that belong together), which variable to use to sort data into different columns, and which variable contains the data values (that will eventually be plottted).

Here is how it works for converting the brother/sister heights longform data into wideform:

heightDataWideform = heightDataLongform.pivot(index='familyID', columns='sex', values='height')
heightDataWideform

sex	Female	Male
familyID
118173	165	172
136536	169	170
165826	179	181
185965	172	175
218511	159	161
260033	148	154
327878	177	181
330754	180	172
342207	172	180
410119	172	174
427440	163	169
438181	180	183
483548	165	175
565176	170	175
578843	176	180
608784	188	195
626851	157	162
700114	175	189
714099	168	175
809371	176	180
819334	171	173
902900	160	161
934515	159	167
936244	164	172
992816	164	169

	brother	sister
0	174	172
1	183	180
2	154	148
3	172	180
4	172	165
5	161	159
6	167	159
7	172	164
8	195	188
9	189	175
10	161	160
11	181	177
12	175	168
13	170	169
14	175	165
15	169	164
16	169	163
17	180	176
18	180	176
19	180	172
20	175	170
21	162	157
22	175	172
23	181	179
24	173	171

	brother	sister
0	174	172
1	183	180
2	154	148
3	172	180
4	172	165
5	161	159
6	167	159
7	172	164
8	195	188
9	189	175
10	161	160
11	181	177
12	175	168
13	170	169
14	175	165
15	169	164
16	169	163
17	180	176
18	180	176
19	180	172
20	175	170
21	162	157
22	175	172
23	181	179
24	173	171