5.3. Odds, logs and log odds#
What are ‘odds’?
Click to reveal answer
In everyday language, the term odds is used interchangeably with probability. But in statistics, there is a specific definition. Let’s imagine a sample of 100 adults in the UK. We find out that 92 of those 100 have had at least one dose of a covid-19 vaccine. The probability is straightforwardly: \(\frac{92}{100} = 0.92\)
But, the odds of observing the outcome are:
So here:
We can interpret the odds to mean that being vaccinated is 11.5 times more likely than not being vaccinated. Note that probability and odds are two ways of expressing the same idea
Say we also have a sample of children aged 5-11. Among these, only 11 of 100 have been vaccinated. In this case the odds are;
If the probability of something is 50-50, what are the odds?
Click to reveal answer
Exactly 1
So, we have seen that a probability >50% produces odds with a value > 1 and a probability <50% produces odds with a value < 1. And when a probability is exactly 50-50 the odds will be exactly 1. We’ll come back to this later when we interpret the output of our logistic regression models.
What’s a “log”?
Click to reveal answer
A log (or logarithm) expresses the inverse of an exponential. If you did A-level maths, this should sound familiar, but if not, here’s quick overview. Exponentials refer to ‘power’ functions, such as \(2^3\) (two to the power of three, also known as two cubed), which means \(2 \times 2 \times 2\) (and equals 8).
\(2^3\) can be expressed as:
Which says that the log base 2 of 8 is equal to 3.
More generally, when \(a^b = c\) then \(\log_a{c} = b\)
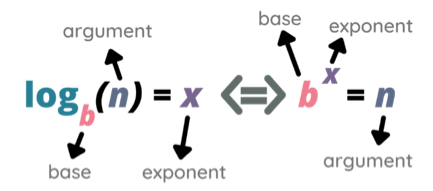
Can you express \(10^3\) as a log?
Click to reveal answer
\(\log_{10}{1000} = 3 \)
Let’s try this one, \(\log_2{16} = x\). What is \(x\)?
Click to reveal answer
A: The question we are trying to solve is: two to the power of what equals 16? The answer is 4 (because \(2^4 = 16\)).
On Canvas, you’ll find additional materials on logs, if you need them.
In our examples above, we have seen log base 2 and log base 10 (these are the easiest to work with for working out in your head). Instead of using 2 or 10, the logit function in logistic regression uses the “natural logarithm” or \(\log_e\) where the base is the constant \(e\) which is much used in maths and statistics. \(e\) has a value of 2.718 and is known as Euler’s number or Euler’s constant. You don’t need to worry too much about why this is the way it is done, or where Euler’s constant comes from, but this is what is going on in our logarithmic transformation. (For the curious, there is an easy video on Canvas about Euler’s constant). The natural logarithm is often written as ln.
Can you figure out what the answer to this one would be?
Click to reveal answer
\(x=0\) (because anything to the power of zero = 1).
