3.4. Conditional Distributions

Conditional distributions refer to spread of value around the regression line.

In this example, where \(y\) = income, and \(x\) = years of education, the expected value of income = -5000 + 3000*years of education.

For people with 12 years of education (\(𝑥\) = 12), the expected mean income is 31,000.

However, we can think of the predicted value as a predicted mean, and that there will be a normal distribution of values around that mean. The word ‘conditional’ here refers to the distribution of \(y\), conditional on a given value of \(x\).

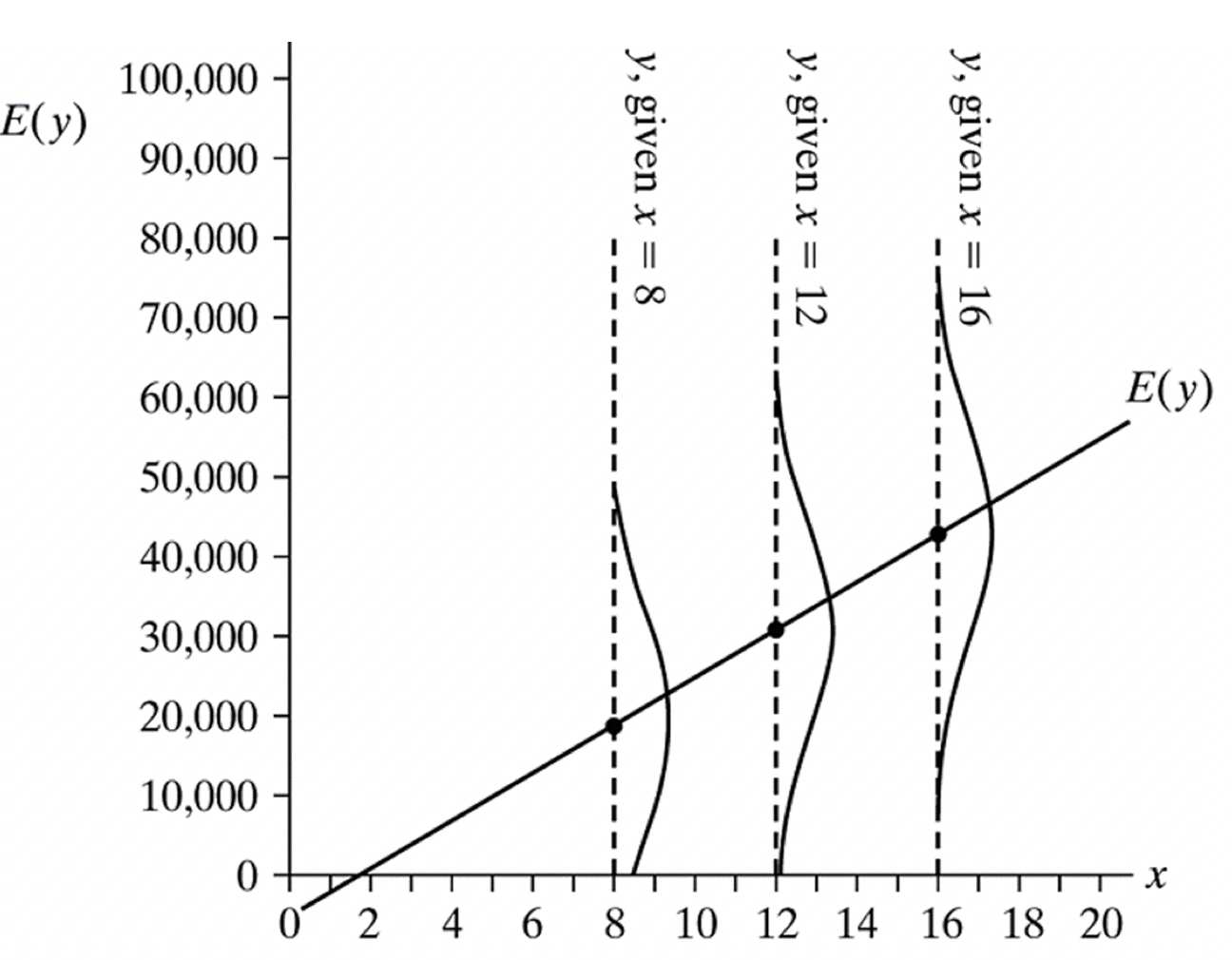
We can use a statistic called the “Root mean square error” (Or RMSE) to estimate spread around the regression line.

The RMSE provides the estimated standard deviation of conditional distribution of \(y\) at each value of \(x\). It is also known as the standard deviation of the residuals.

The equation for the RMSE is:

\[ \sqrt{MSE} = s_y\sqrt{1-r^2} \]

Again, you’ll notice that it is comprised of familiar components, namely, the standard deviation of \(y\), and \(R^2\).

• Coming back to the immigration data from last week, where \(s_y\) = 2.533, and \(r\) = -0.1572, plug these values into the equation and find the RMSE.

Click to reveal answer

\[RMSE = 2.533\sqrt{0.975288)} = 2.50\]

• How do we interpret the RMSE?

Click to reveal answer

We expect 95% of the values of \(y\) at a given \(x\) to fall within 1.96 standard deviations of the mean.

• note that if the sample size were smaller, we would not use 1.96, which is the critical value of \(t\) for \(\alpha=0.05\) and for large sample sizes (over about 50). Instead we would use the critical values of \(t\) is for \(\alpha\)=0.05 and out actual sample size - there is a section on \(t\) confidence intervals in the final lecture from Michaelmas Term.

Let’s look at an example when \(x\) = 65. The regression line gives us a mean expected answer to the immigration question of 5.380 (based on the equation \(\hat{y}=6.790-0.0217\times age\)).

5.380 \(\pm\) (1.96*2.50) = [0.480, 10.280]

When \(x\) = 65, we expect 95% of values to fall between 0.480 and 10.280, which is a wide spread of values around the regression line.