1.5. Statsitical Independence

If two events are statistically independent, it means that the outcome of one event does not affect the outcome of the other.

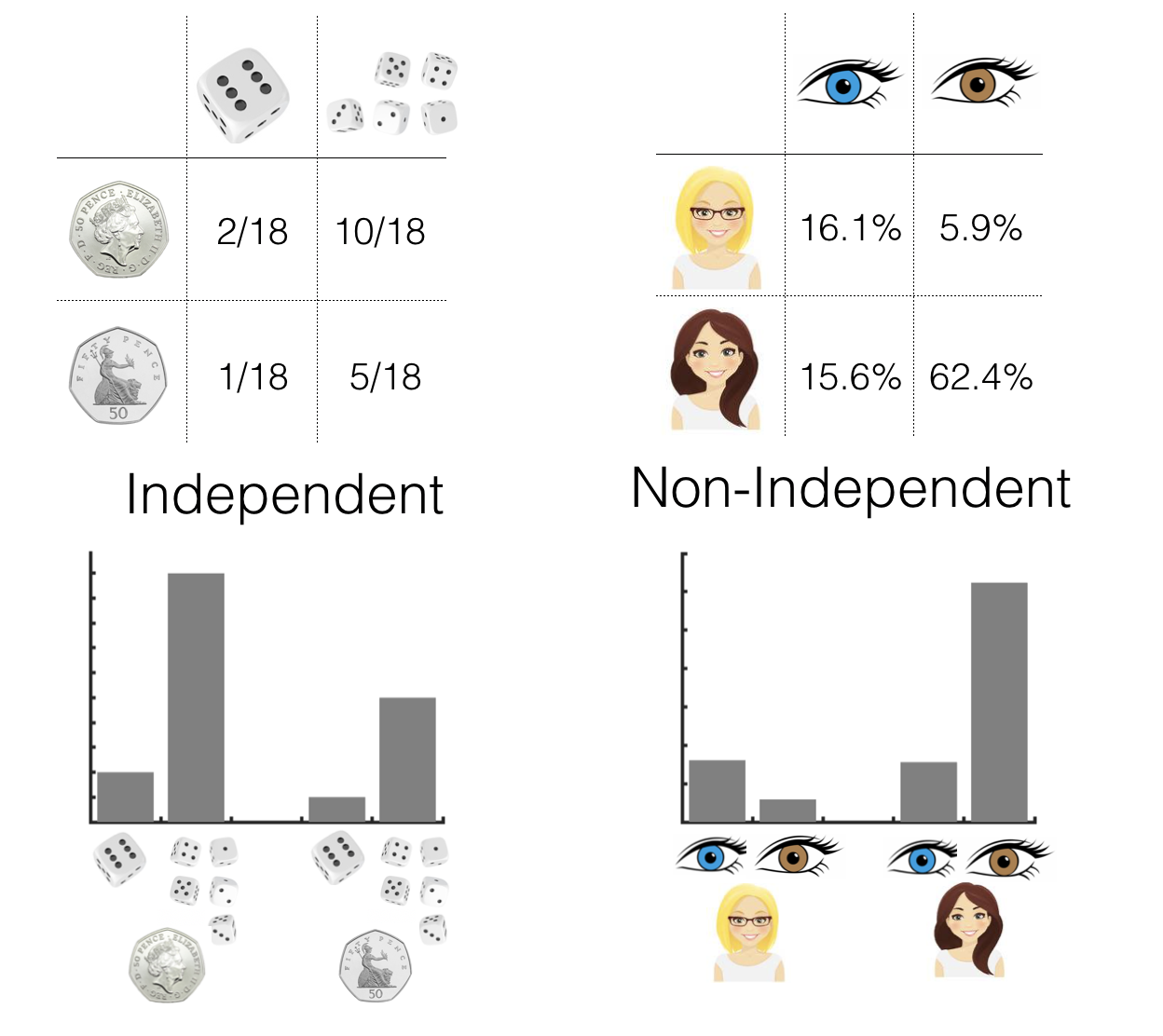
For example, if we toss a coin, the roll a dice, the outcome of the coin toss does not affect the outcome of the diceroll.

In contrast, we can think about events which are not independent because a common factor influences both events. For example, is a person’s hair colour independent of their eye colour? In the UK, people are more likely to have blue eyes if they also have blond hair, since common genetic factors cause both these features.

In the probability tree, we see the difference between independent and non-independent events by looking closely at the probabilities after the second branch point.

• The probability of rolling a 6 is always one sixth, both in the case that teh coin toss yeilded heads, and tails.

• The probability of blue eyes is quite difference for blond and non-blond individuals; blond people are more likely to have blue eyes that not, but non-blond people are unlikely to have blue eyes.

We can also look at independent vs non-independent events in a contingency table, or a bar plot.

1.5.1. Interaction effects

Note the bar plot in particular - for non-independent events we see an interaction effect - the relative heights of the eye-colour bars differ for the two catgories of hair colour.