3.4. The t distribution#
The \(t\) distribution describes the shape of the best-estimate sampling distribution of the mean when data are drawn from a normal distribution and the best-fitting normal distribution (ie, it mean and standard deviation) have been estimated from a small sample.
3.4.1. Sampling distribution of the mean#
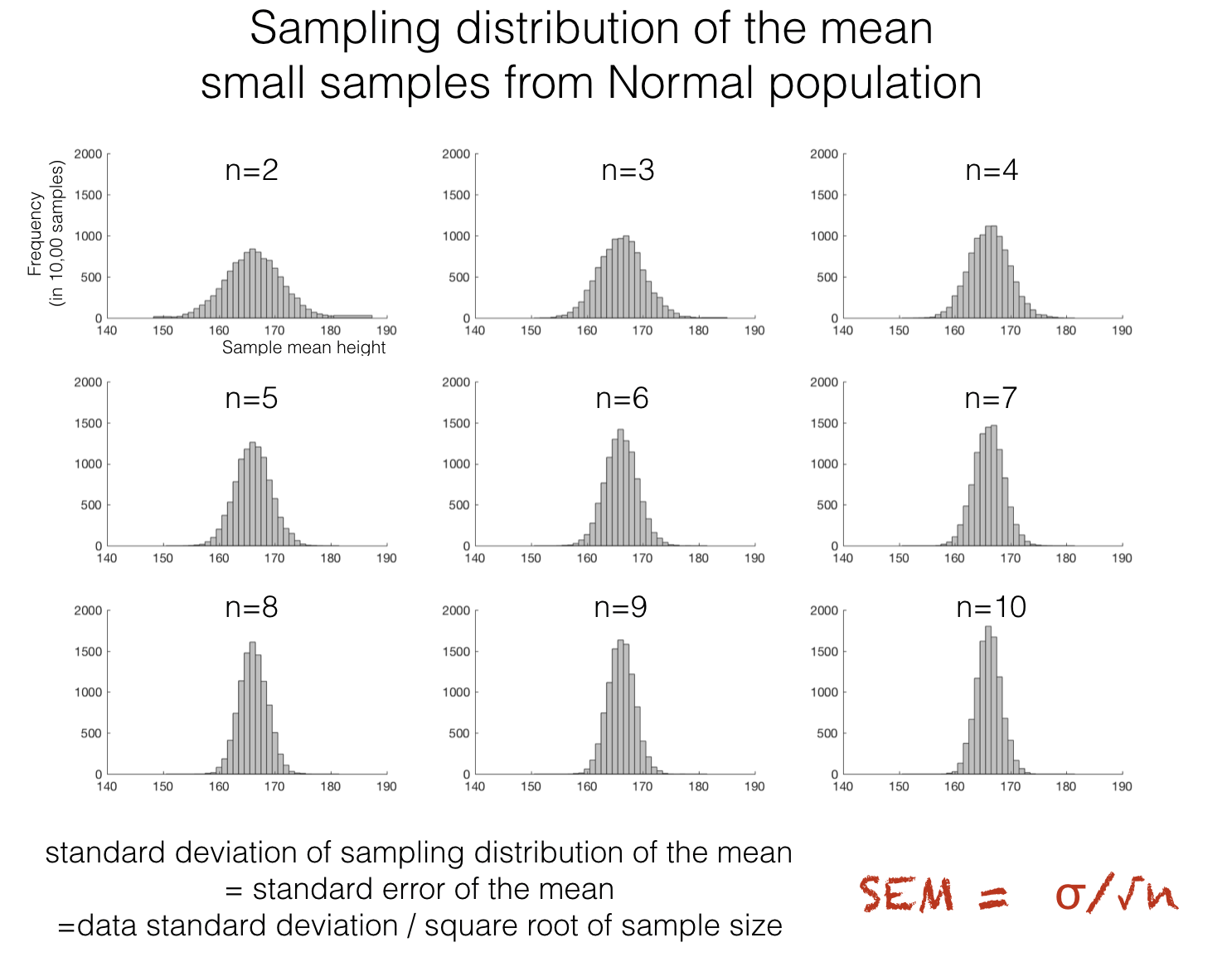
The sampling distribution of the mean is the distribution you would get if you took many different samples of size \(n\) from the population and calculated each of their means
The null distribution is the sampling distribution of the mean (or another test statistic) that we would expect to get if the null hypothesis were true
3.4.2. Scaling by sample size#
Recall from the previous lecture that the spread of the sampling distribution of the mean depends on the sample size. More precisely:
The standard deviation of the sampling distribution of the mean is the standard error, \(s/\sqrt{n}\) where \(s\) is the sample standard deviation and \(n\) is the sample size
3.4.3. Pointy top, heavy tails#
The \(t\) distribution looks a lot like the normal distribution, but it has a pointy top and heavy tails.
The \(t\) distribution actually changes shape depending on the sample size used to fit the best-fitting normal:
when the sample is tiny (\(n=2\)) we get an extreme pointy top and heavy tails
as the sample size gets large (about 30) the t distribution is almost identical to the normal distribution
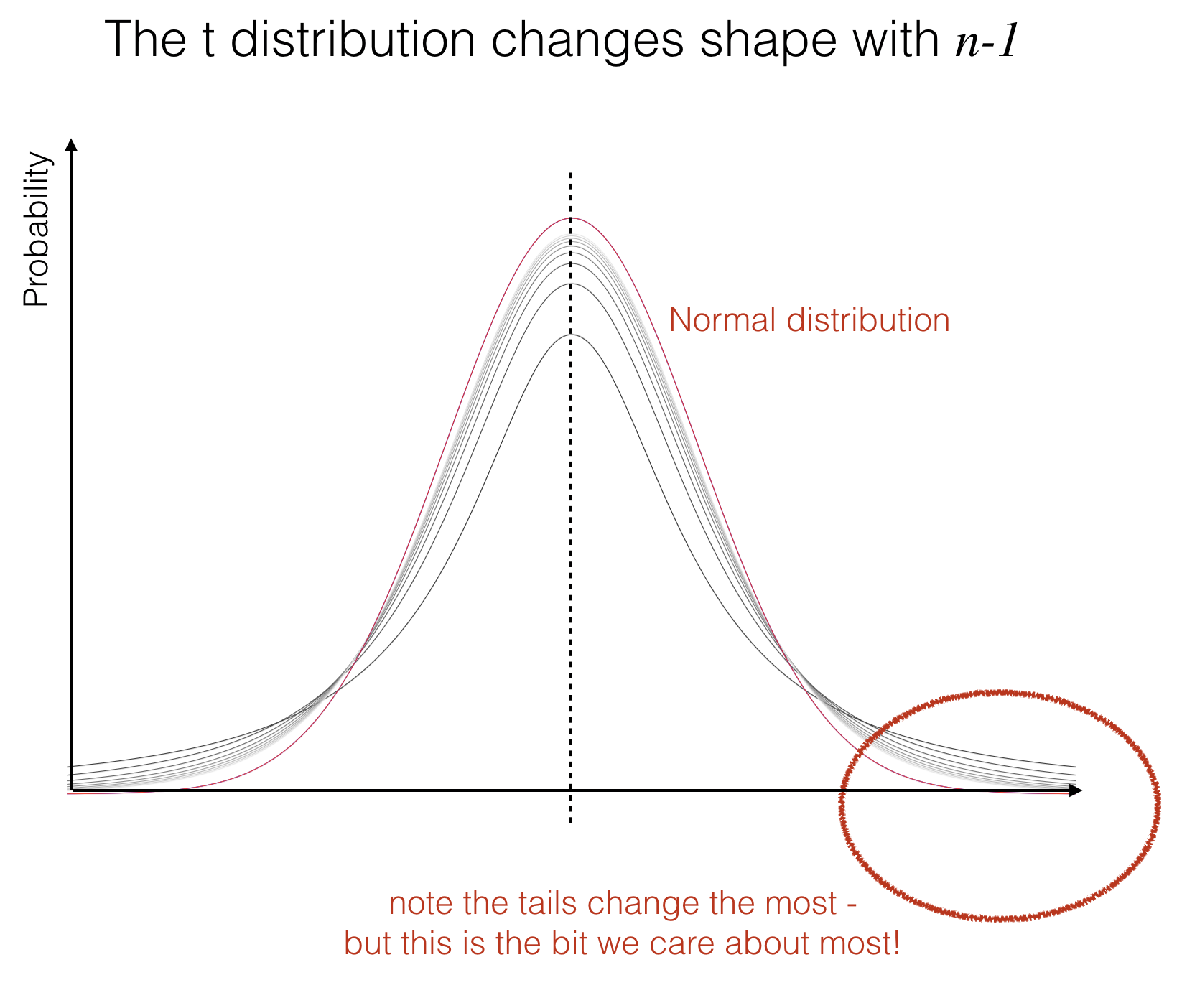
This distinction may appear subtle but remember that when a value is statistically significant, it lies in the tails of the null distribution. So if the \(t\)-distribution is the sampling distribution of the mean under the null hypothesis, we will be looking closely at its tails to determine the probability that our result (difference of means) could have arisen due to chance.
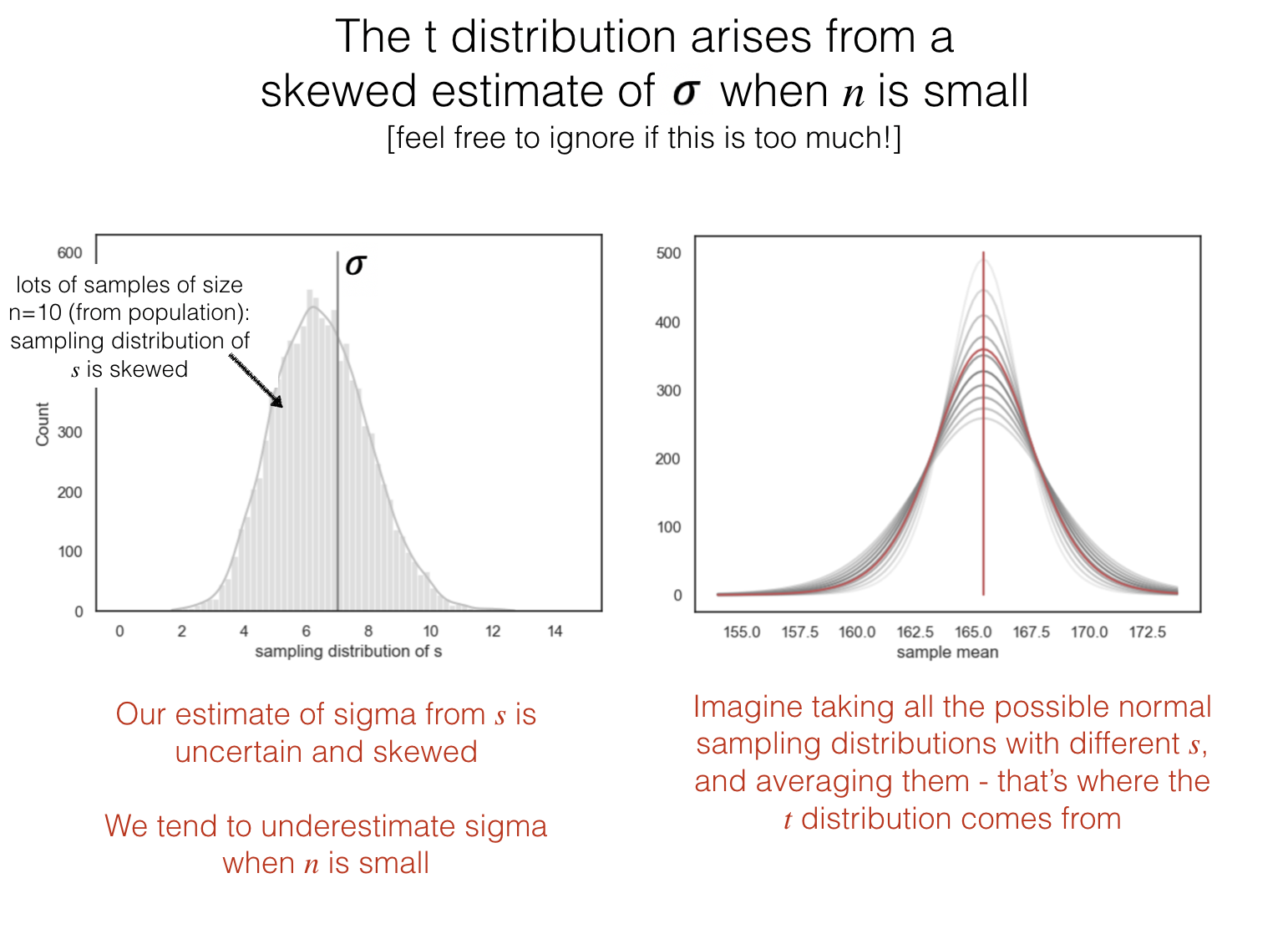
Why heavy tails?#
You can skip this bit if you don’t fancy it; it is sufficient to understand that the \(t\)-distribution has heavy tails because of ‘something to do with estimating the standard deviation’!
3.4.4. Analogy: \(t\) and \(Z\)#
We saw that if data are normally distributed, that when we standardize data by converting the data to Z-scores, we create a distribution (of Z) with a fixed mean (zero) and standard deviation (1). If the data mean is \(\bar{x}\) and standard deviation \(s\):
From this standardied distribution, we can directly read off the probability of a given data value (eg the probability ot a Z-score greater than 1 is 15%)
Similarly for sample means, if we standardize by converting to \(t\)-scores:
This standardized distribution tells us the probability of a sample mean as large as our observed one \(\bar{x}\) (or larger) if the population mean was really zero
This is the probability of the sample mean arising due to chance under the null hypothesis, if the null hypothesis is that the population mean is zero.
3.4.5. Link to t-test#
Of course, we don’t always expect our population mean to be zero under the null hypothesis. In the following sections, we see three examples
Single sample t-test#
Under the null, \((\bar{x}-\mu) = 0\), where \(\mu\) is a reference value and \(\bar{x}\) is the sample mean.
For example we hypothesise that Oxford students’ IQs are higher than the average (by definition the average IQ is 100)
\(\mathcal{H_o}\): Oxford students’ mean IQ is 100 \(\mathcal{H_a}\): Oxford students’ mean IQ is greater than 100
Then our equation to get the standardied \(t\) becomes:
Paired samples t-test#
Under the null, \((\bar{x-y}) = 0\), where \(x\) and \(y\) are paired values such as brothers’ and sisters’ heights, and \((\bar{x-y})\) is the mean difference in height between a brother and his own sister.
For example we hypothesise that men are taller than women:
\(\mathcal{H_o}\): The mean brother-sister difference is 0 \(\mathcal{H_a}\): The mean brother-sister difference is greater than 0
Then our equation to get the standardied \(t\) becomes:
Independent samples t-test#
Under the null, \((\bar{x}-\bar{y}) = 0\), where \(x\) and \(y\) are independent samples, and \(\bar{x}\) and \(\bar{y}\) are the means of those independent samples.
For example we hypothesise that Oxford students’ IQs (\(x\)) are higher than Cambridge students IQs (\(y\))
\(\mathcal{H_o}\): Difference of means is zero \(\mathcal{H_a}\): Difference of means (Oxford-Cambridge) is greater than zero
Then our equation to get the standardized \(t\) becomes:
… noting that \(s\) is now a combined standard deviation measure based on both samples, sommetimes called the ‘pooled variance estimate’; you don’t need t worry about how to calculate this as it is done automatically when you run the independent samples \(t\)-test in scipy.stats.
