2.4. Difference of medians vs difference of means#
When we state the null and alternative hypotheses for our rank-based tests, we refer to a difference in medians rather than a difference of means:
\(\mathcal{H_o}\): there is no difference in median salary between men and women \(\mathcal{H_a}\): the median salary of men is higher than that of women
Why is this?
2.4.1. After ranking the data, we don’t know what the mean is any more!#
Consider the following two datasets, which have very different means, but after ranking are identical:
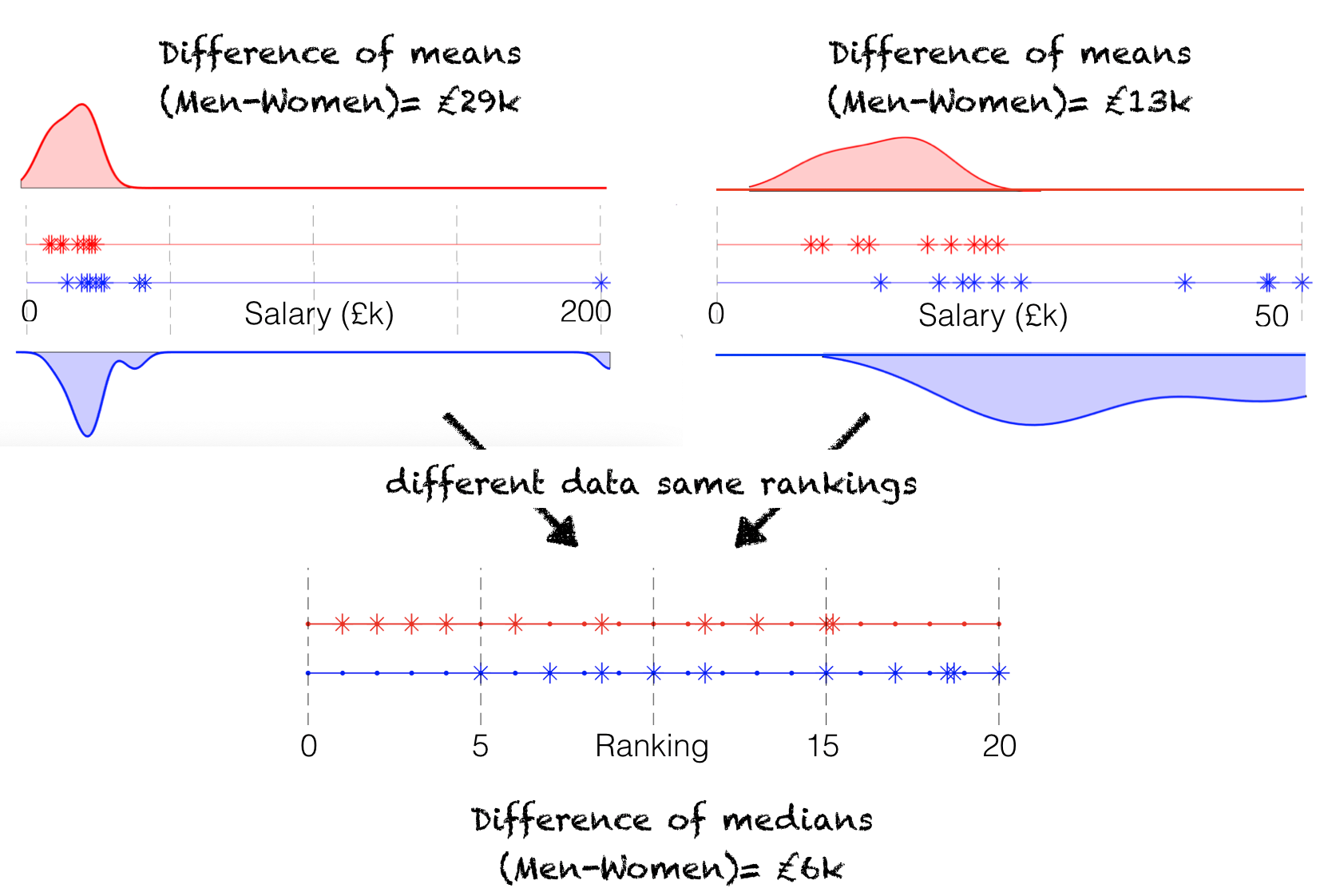
Our rank-based statistical tests only use the ranks, not the original data. The difference between groups in the left- and right datasets would be equally significant based on a rank-sum test, even though the difference of means is much greater (and would be more statistically significant) in the dataset on the left.
Therefore it would be incorrect to say that a rank-based test is testing for a difference in means - in fact it is not sensitive to a difference in means as long as the ranks remain unchanged (as in the two datasets above).
On the other hand, the ranked data do directly relate to the median, which by definition is simply the middle-ranked value
