4.5. Effect size (Pearson’s r)#

The effect size for a correlation is quantified simply by the correlation coefficient Pearson’s $r$.

Remember an effect size tells us how large the effect of interest is, in comparison to random variation.

In the case of a correlation, the effect of interest is the relationship between $x$ and $y$ along the best-fit line $y=mx+c$, whilst the random variation is the spread of data about this line

Pearson’s $r$ quantifies exactly that - remember this figure from the section on Correlation in the chapter on Describing Data (you may like to look back at it):

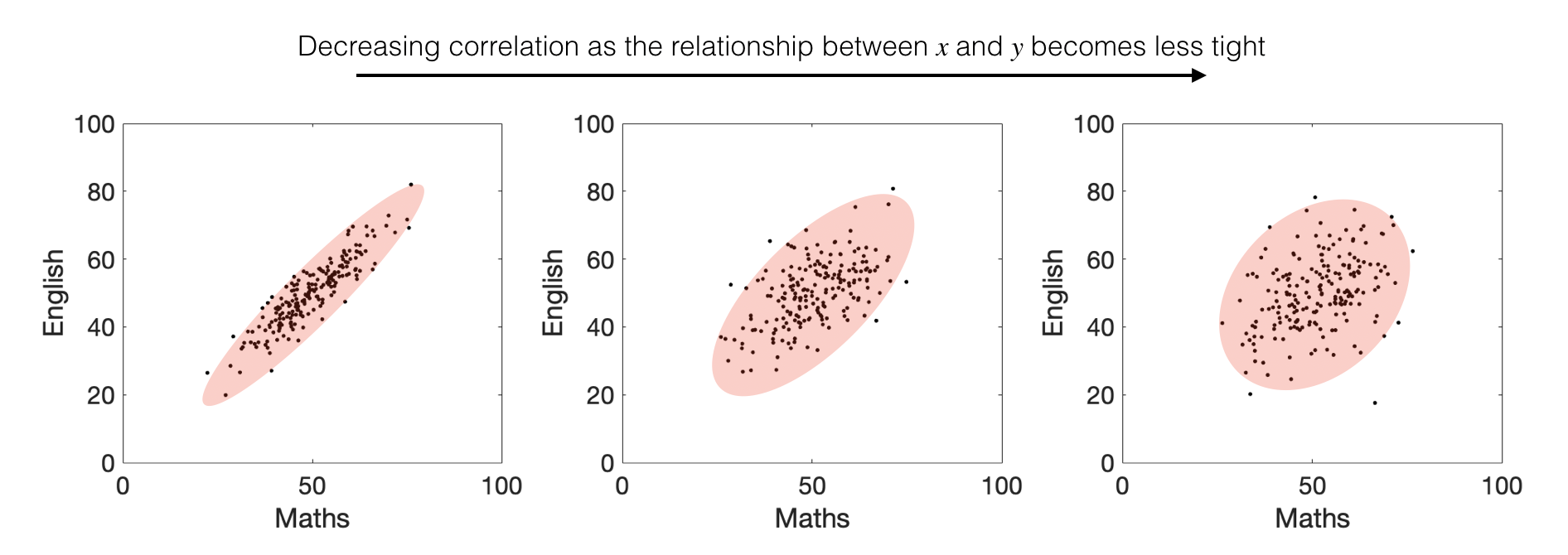
The correlation coefficient $r$ is always a number between 1 (perfect positive correlation; all points on a line) and -1 (perfect negative correlation)

Correlation gives us a ‘pure’ measure of the strength of the relationship between $x$ and $y$ (corrected for the spread within $x$ and $y$ independently).

4.5.1. Effect size $\ne$ statistical significance#

Note that for any given correlation, whether it is believable or statistically significant also depends on the sample size $n$.

Consider the following examples:

• the top row all have sample size $n=12$

• the bottom row have sample size $n=200$

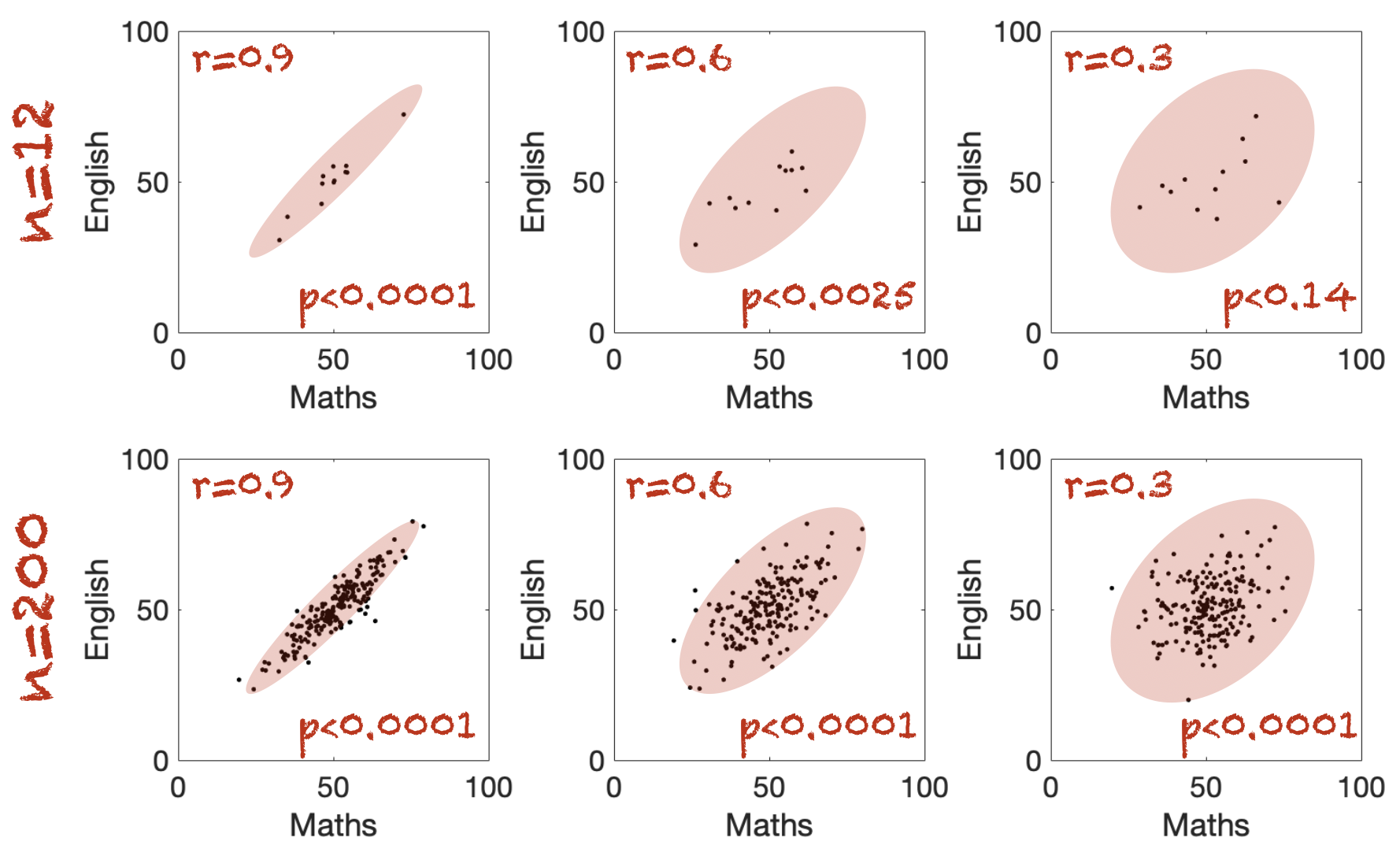
The red oval captures the shape of the dot cloud; an elongated shape is a stronger correlation and greater effect size.

Nonetheless, for a given effect size, the correlation is less convincing for small $n$ - this is reflected in the statistical significance ($p$ values).

Statistical significance of $r$#

For a given values of Pearson’s $r$, we can actually test the significance of the correlation using a one-sample $t$-test.

We calculate a $t$-score using the equation:

$$t=\frac{r\sqrt{n-2}}{\sqrt{(1-r^2)}}$$

and then the $p$-value is obtained from the $t_{n-2}$ distribution.

However you can get straight to the $p$-value by using scipy.stats - note that we are using scipy.stats as the other correlation functions we met in numpy and pandas do not return a $p$-value.

Here is the syntax to test the correlation between Maths and English scores, assuming these are columns in a dataframe scores:

stats.pearsonr(scores.maths, scores.english).pvalue

What counts as a large effect#

Wikipedia tells me that $r$ values of 0.1, 0.3 and 0.5 are considered small, medium and large respectively

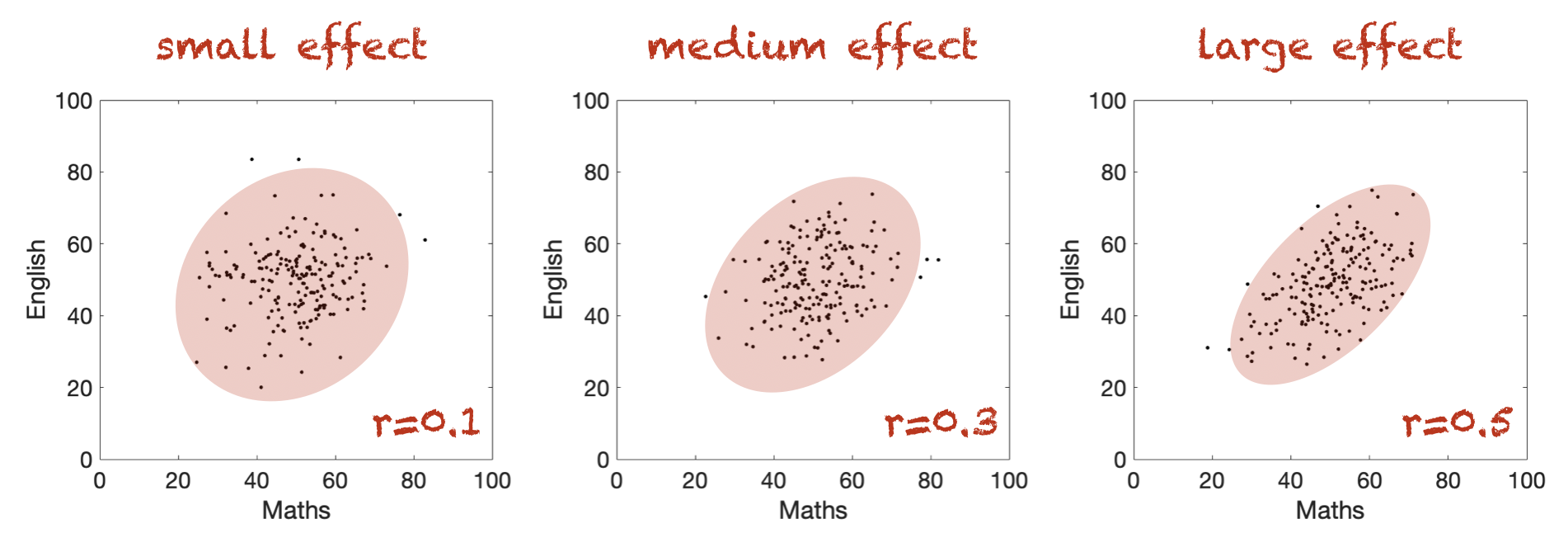
… but bear in mind this is just a rule of thumb.