3.3. Best fitting Normal#
If we have some data \(x\), and we believe they come from a normal distribution, we can describe the normal distribution thhey most likely came from as \(x \sim \mathcal{N}(m, s)\) where \(m\) and \(s\) are the mean and standard deviation we calculated from the data.
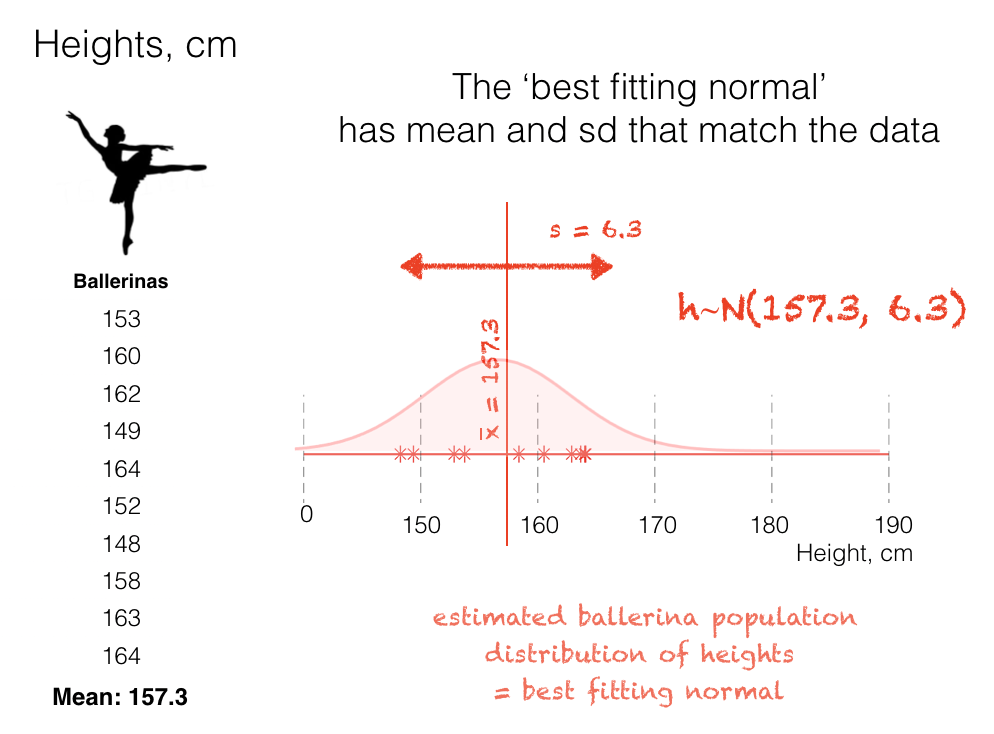
For example, given the heights of 10 fictional ballerinas, we can calculate the sample mean (157.3cm) and sd (6.3cm).
From these two numbers, we can reconstruct an estimate of the height distribution for all the ballerinas in the world (!) as the normal distribution with the matching mean and standard deviation, AKA the best fitting normal
3.3.1. By fitting the Normal we gain some information#
If it is correct that heights are normally distributed, we should have a quite precise model of the heights of ballerinas worldwide by fitting the best-fitting normal to our data. Importantly this should be more ‘correct’ than assuming that heights in the population have the same distribution as in the sample (which is not perfectly normal)
Compare the best fitting normals to the data KDE for ballerinas:
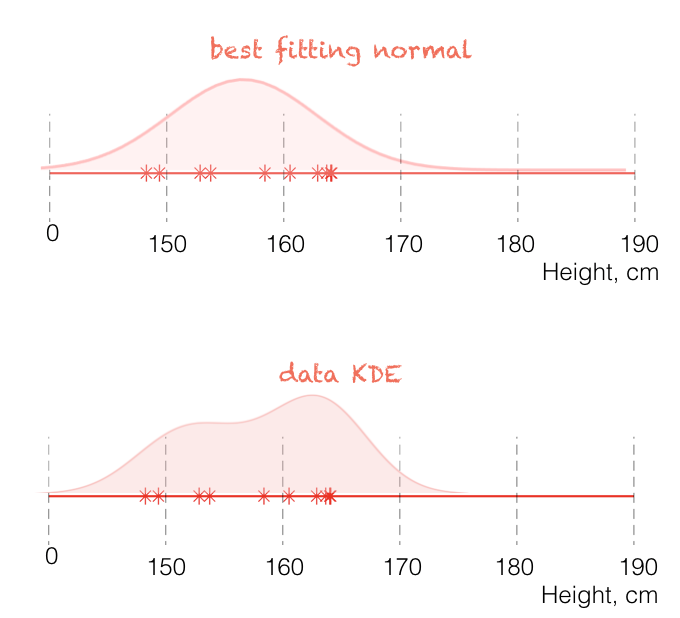
If it is true that heights in the population of ballerinas are normally distributed, the best fitting normal should be a more accurate estimate of the population height distribution; the double mode in the KDE is a quirk of the small sample (10 ballerinas) that we measured.
3.3.2. Incorrect assumption of normality#
If the data are not really drawn from a normal distribution, the best fitting normal will be a poor estimate of the population data distribution.
Often non-normal data distributions have outliers that would be really implausible under the normal distribution, and if we try to fit a normal to such data it ends up needing to be very wide to accommodate the outliers.
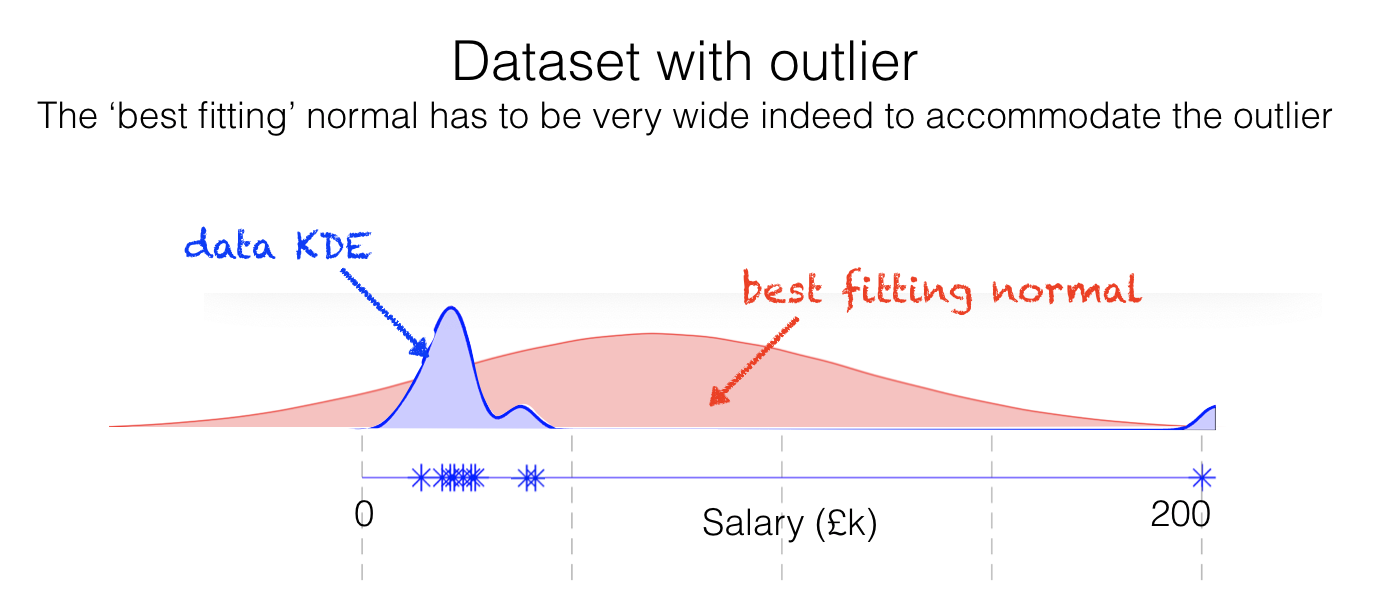
in the salary example shown above, the best fitting normal suggests that the most common salary is about £80k and that many people earn negative amounts of money - clearly not a good match to the sample data, or a plausible estimate of the salaries in the population as a whole!
3.3.3. The best fitting normmal is just an estimate#
The best fitting normal is a normal distribution whose mean and standard deviation \(m\) and \(s\) are calcaulted from the data.
Of course, even if the data are drawn from a normal population, it is likely that the data mean and standard deviation in a small sample are not exactly the same as the mean and standard deviation of the population as a whole (because samples are random and we may happen to sample, for example, more tall or short ballerinas than we ‘should’).
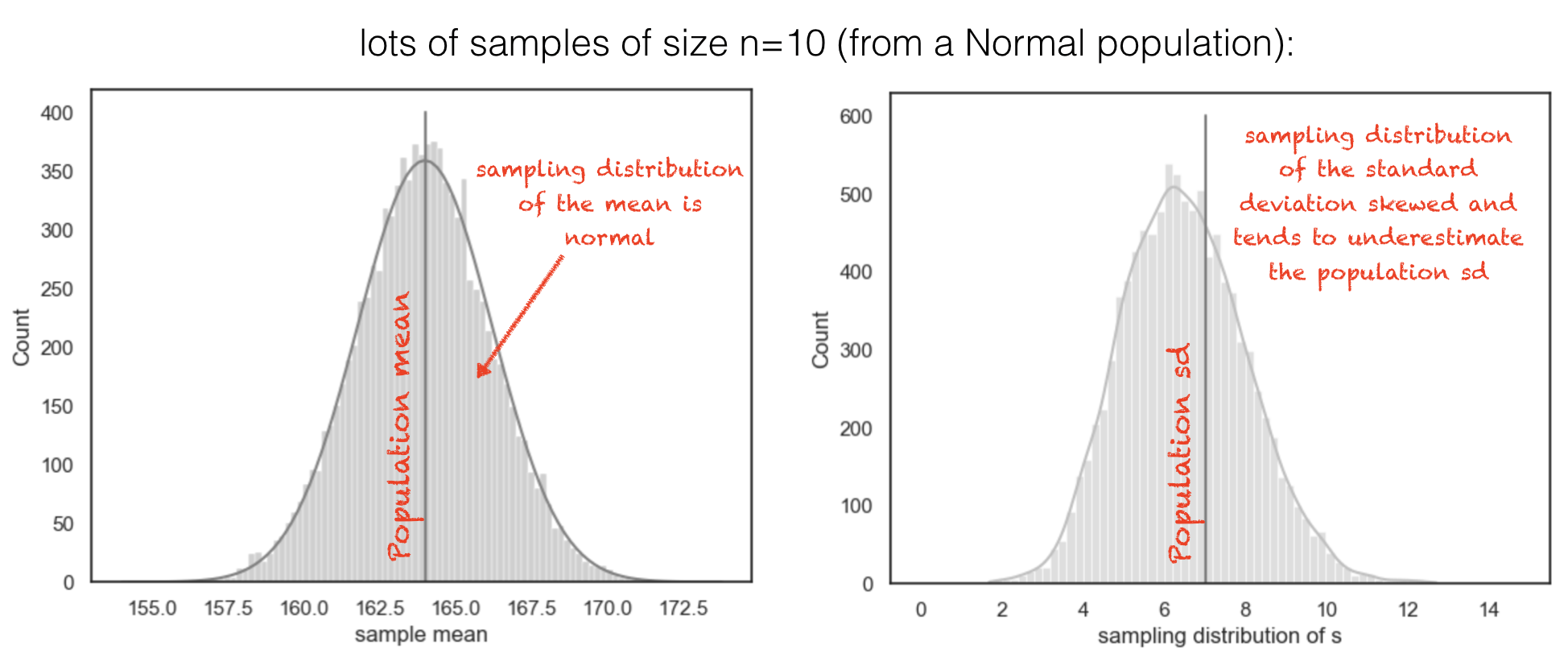
Below I drew 10,000 samples of size \(n=10\) from a large population of normally distributed values, and calcluated the mean and standard deviation of each sample
sample means are normally distributed and centred on the true population mean
sample standard deviations have a skewed distribution and tend to underestimate the population standard deviation
Most importantly:
the sample mean and standard deviation are just estimates of the population mean and standard deviation and vary randomly from sample to sample