5.1. The Binomial Distribution#

Consider the following situations:

  • a fair coin is tossed 10 times. How likely is it that we obtain exactly 5 heads?
  • a fair six sided dice is rolled 3 times. How likely is it that we obtain two or more sixes?
  • a blind man guesses whether a symbol on a screen is an X or an O. How likely is it that he guesses correctly at least 22 out of 30 times?

In each case there is an event with two possible outcomes.

One outcome (the one we are looking for) is designated as a “hit” whilst the other is called a “miss”.

The probability of a hit is a fixed value (p)

The event is repeated a certain number of times (n) and we count the number of times (k) one of the outcomes (the “hit”) occurs

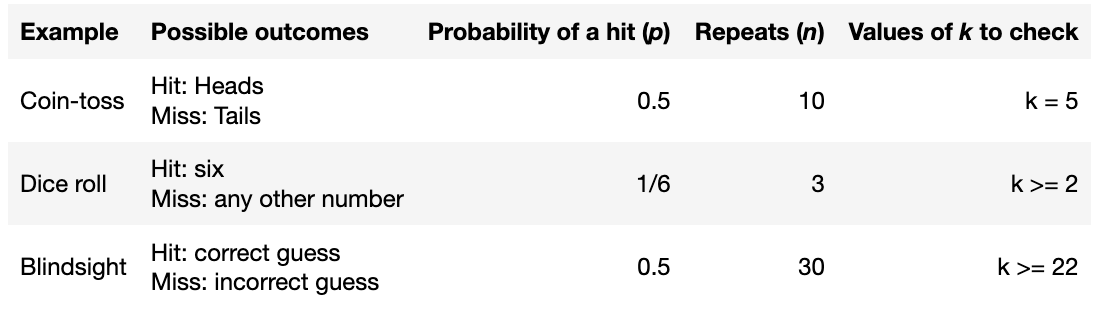
talbe of examples

In each case we can ask, what is the probability of obtaining k (or at least k) hits out of n trials, given that the probability of a hit on any given trial is p?

The probability of each value of k is given by the inomial distribution