16.3. ANOVA Concepts#

Analysis of Variance (ANOVA) is a test of independence where the outcome variable is continuous, and the explanatory variable is categorical. It is a way of comparing means across groups and is preferred where there are more than two groups. If we ran an experiment with three groups – say treatment1, treatment2, and control group - ANOVA enables the researcher to test the means of these three groups simultaneously.

  • If there were only two groups, which test would you use to compare means?

Click to reveal answer

The $t$-test. We use ANOVA when there are more than two groups.

  • Why is a comparison of means called Analysis of Variance?

Click to reveal answer

ANOVA uses the variance to compare means.

It compares the variability between the overall mean $\bar{y}$ and the group means $\bar{y_i}$ (where subscript i means ‘in each group’) with the variability within each group $\bar{y_1}, \bar{y_2}, \bar{y_3}$ etc. (where subscript 1 means ‘in group 1’ and so on).

Look at the example dataset below, from Agresti and Finlay (Figure 12.1)

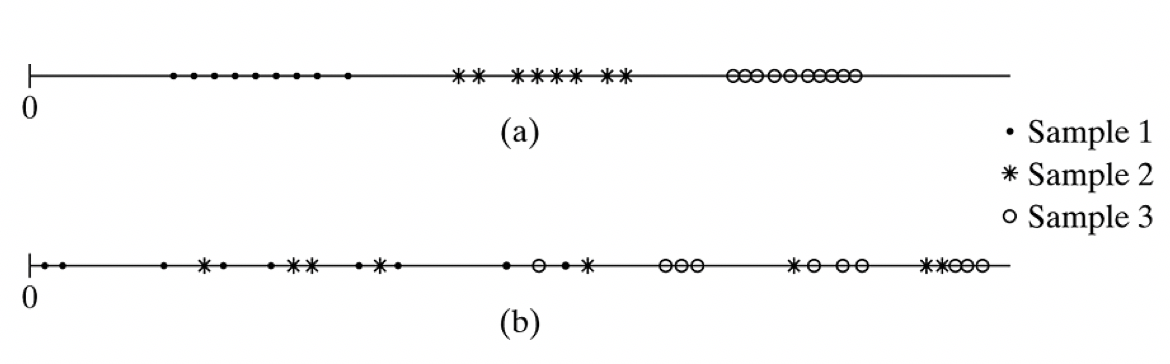
https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook/main/images/regression4_AgrestiDataset.png

The means of the three groups in a are clearly different to each other.

In b there is more overlap between the data points, and it is harder to tell just by eyeballing the data whether there is a difference in means in the three groups.

In this example, the means of the three groups, and the overall mean, are the same in a and b which means that the variability between groups is the same in a and b. However, the variability within groups is lower in a than in b. Low variability within groups suggests that the groups have means that are statistically different to each other.

ANOVA uses the $F$-statistic to test whether there are significant differences in means across groups. The $F$-statistic is a ratio of the between-groups variance divided by the within-group variance as follows:

$$ F = \frac{\textrm{Between-groups estimate of variance } σ^2}{\textrm{Within-groups estimate of variance } σ^2} $$

  • What does it mean when the $F$-statistic is large?

Click to reveal answer

The $F$ test statistic is large if variability between groups is large relative to variability within groups.

Looking back to the example above, where the within-group variability is lower in a than in b, we would expect a larger $F$ value in a than in b. Larger $F$ values have smaller $p$-values and indicate that there is a difference between groups. The cut-off value for $F$ (i.e., what counts as ‘large’) depends on the degrees of freedom (sample size and number of groups). When you run ANOVA in a stats package such as Python, it will produce the $p$-value for you.

  • What are the assumptions of ANOVA?

Click to reveal answer

The three assumptions are:

  • For each group, the population distribution of the response variable $y$ is normal.

  • The standard deviation of the population distribution is the same for each group. Denote the common value by $\sigma$

  • The samples from the populations are independent random samples.

  • What is the non-parametric equivalent of ANOVA?

Click to reveal answer

The Kruskal-Wallis test.

The Kruskal-Wallis test ranks the observations and compares mean ranks of the groups, thus uses only ordinal information in the data.