3.6. Scatterplot

If we want to see the relationship between paired measurements, a scatterplot is a good choice

Examples would be:

• Heights of brothers and sisters
• A patient's blood pressure before and after taking a drug
• Reaction time on the same task with and without distraction

Example: brother/sister heights

A researcher hypothesises that men are taller than women.

He also notices that there is a considerable genetic influence on height, with some families being taller than others

He decides to control for this by comparing the heights of brothers and sisters (shared genetic influence, shared upbringing). This is a paired design.

Set up Python libraries

As usual, run the code cell below to import the relevant Python libraries

# Set-up Python libraries - you need to run this but you don't need to change it
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pandas 
import seaborn as sns
sns.set_theme()

Load and inspect the data

Load the file BrotherSisterData.csv which contains heights in cm for 25 brother-sister pairs

heightData = pandas.read_csv('https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook/main/data/BrotherSisterData.csv')
display(heightData)

	brother	sister
0	174	172
1	183	180
2	154	148
3	172	180
4	172	165
5	161	159
6	167	159
7	172	164
8	195	188
9	189	175
10	161	160
11	181	177
12	175	168
13	170	169
14	175	165
15	169	164
16	169	163
17	180	176
18	180	176
19	180	172
20	175	170
21	162	157
22	175	172
23	181	179
24	173	171

Independent KDE plots

Let’s use a KDE plot to compare the heights of the men (brothers) and women (sisters) in the sample.

We can call KDE plot twice to plot the data from brothers and sisters overlayed

sns.kdeplot(heightData["brother"],  color='b',  fill='true', label='brother')
sns.kdeplot(heightData["sister"],  color='r',  fill='true', label='sister' )
plt.xlabel('height (cm)')
plt.legend()

<matplotlib.legend.Legend at 0x7ff21a937df0>

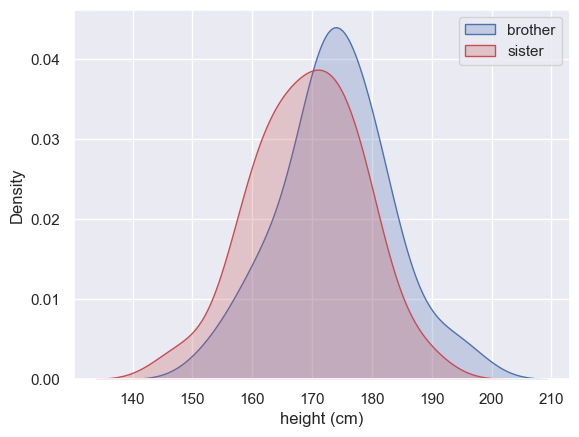
There’s a lot of overlap for sure, and just a hint that the men are taller than the women.

But comparing all the men to all the women is wasting the power of our paired design!

Scatterplot

On a scatterplot, each dot represents two paired datapoints - a brother and sister:

sns.scatterplot(x=heightData["brother"], y=heightData["sister"])

<Axes: xlabel='brother', ylabel='sister'>

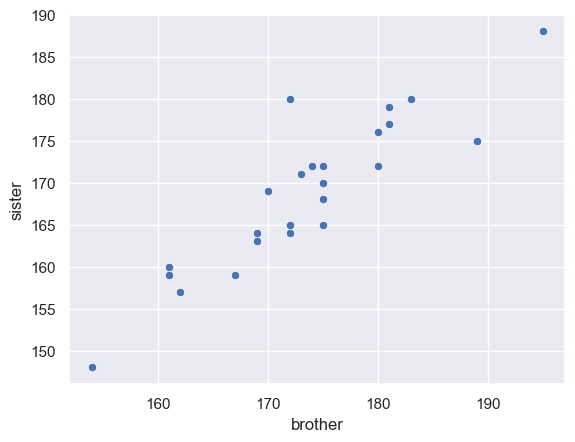
One thing we can clearly see is that tall brothers tend to have tall sisters - that is there is a shared familial effect, or to put it another way, height of brothers aand sisters is correlated across families.

This suggests it was a good idea to use a paired design as what we really want to know is not whether some families are taller than others, but whether the male sibling in each family is taller than the female sibling once the family effect is accounted for (by compaaring only within families). To help us visualise this we add a reference line

Reference line

Let’s add the line x=y to help us interpret the data.

If all the brothers were exactly the same height as their sisters, we would expect all data points to fall exactly on the line x=y

If brothers were roughly the same height as their sisters (with some random variation) we would expect the data points to fall equally often above and below the line x=y

If brothers are generally taller than their sisters, most of the datapoints will fall on one side of the line (think about which!)

To add the line x=y we use the matplotlib function plot. The arguments of this function are the x and y values for the ends of the line (x and y both range from 150-190), and the argument ‘k–’ which sets the color and line type.

• See if you can add another line of code to draw a red horizontal line at y=170

sns.scatterplot(x=heightData["brother"], y=heightData["sister"])
plt.plot([150, 190],[150, 190], 'k--')
#plt.plot([150, 190],[150, 190], 'r:') 
# edit this code to plot a horizontal line at y=170, 
# that is a line between [150 190] in x and [170 170] in y

[<matplotlib.lines.Line2D at 0x7ff21ac84340>]

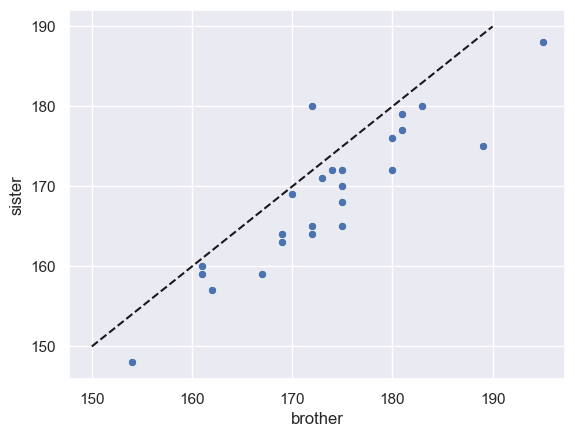
In fact, most of the datapoints fall on one side of the line (below it)

• This means either than most of the brothers are taller than their sisters, or vice versa - which is it (look at the graph)?

Correlation

Notice that in the scatterplot, the data points are spread out along the line x=y.

This means that in general tall brothers have tall sisters and this variation between families rather dwarfs the effect of interest (that within each family the brother is taller than his own sister)

This feature of the plot is evidence that a paired design was a particularly good choice for this question - in the paired design, the (large) variation between families is cancelled out allowing us to detect the (small) difference between male and females.

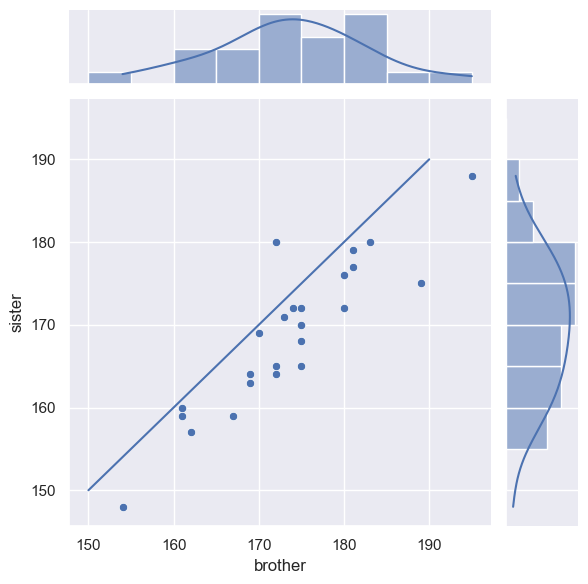
Jointplot

It was nice to be able to see the distribution for each group (brothers and sisters) in the KDE plots, but the KDE plot didn’t show the relationship between brothers and sisters

It was nice to see the relationship between brothers an dtheir sisters in the scatterplot, but it is hard to get a sense of the distribution

We can get the best of both worlds by useing seaborn function jointplot, which shows the marginal distributions (the height distributions for brothers and sisters separately) at the side of the main scatter plot

sns.jointplot(x=heightData["brother"], y=heightData["sister"])

<seaborn.axisgrid.JointGrid at 0x7ff21aecee20>

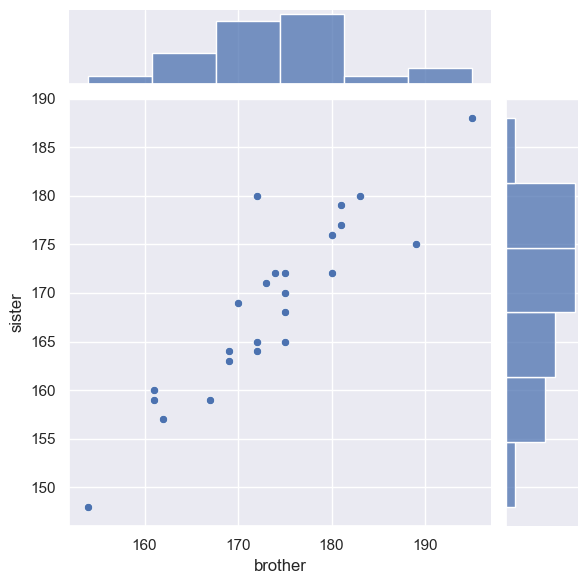
We can adjust the bins and add a KDE plot if we like:

sns.jointplot(x=heightData["brother"], y=heightData["sister"], marginal_kws=dict(bins=range(150,200,5), kde="true"))

<seaborn.axisgrid.JointGrid at 0x7ff21b1fdd30>

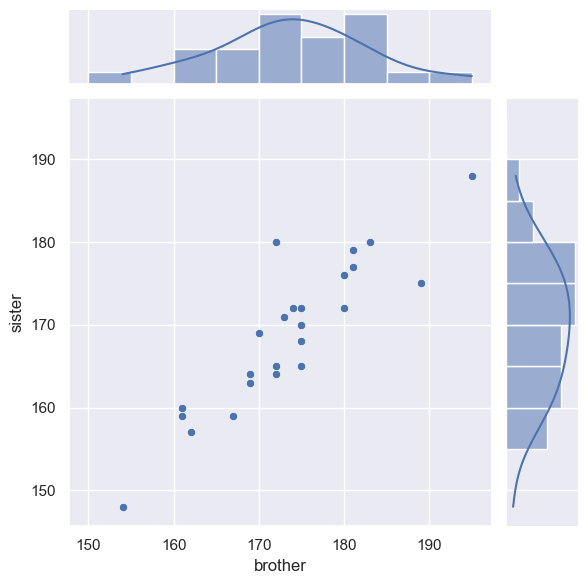
Finally, we can add the line x=y.

This is a little fiddly as we have to tell the computer which part of the the joint plot to add the line to, by getting a handle to the plot (see comments in the code)

# create the joint plot as before but give it a label - "myfig"
myfig = sns.jointplot(x=heightData["brother"], y=heightData["sister"], marginal_kws=dict(bins=range(150,200,5), kde="true"))

# plot the line x=y onto the joint axis (ax_joint) of myfig
myfig.ax_joint.plot([150,190],[150,190])

[<matplotlib.lines.Line2D at 0x7ff21bb67d60>]