1.6. Simulation Exercises

Set up Python libraries

As usual, run the code cell below to import the relevant Python libraries

# Set-up Python libraries - you need to run this but you don't need to change it
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pandas 
import seaborn as sns
sns.set_theme()

Simulated sampling - for loop

Men are taller than women. But if you collect samples of 5 random men and 5 random women, how likely is it that the average height of the women will exceed the average height of the men?

Create some data

We are going to start by creating some fake data (great start to your degree!). These are the heights of 10,000 simulated (made up) men and 10,000 simulated women, which will have the same distribution as the real heights of men and women in the UK.

For today you really don’t need to worry about how I’m creating these simulated heights.

I’m also going to plot a histogram of each distribution - you don’t need to worry about the code for that either as there will be a session on plotting data later on.

men = np.random.normal(175,7, [10000])
women = np.random.normal(162,7, [10000])

sns.histplot(men, color='b', label='men')
sns.histplot(women, color='r', label='women')
plt.legend()

<matplotlib.legend.Legend at 0x7f8add05ad00>

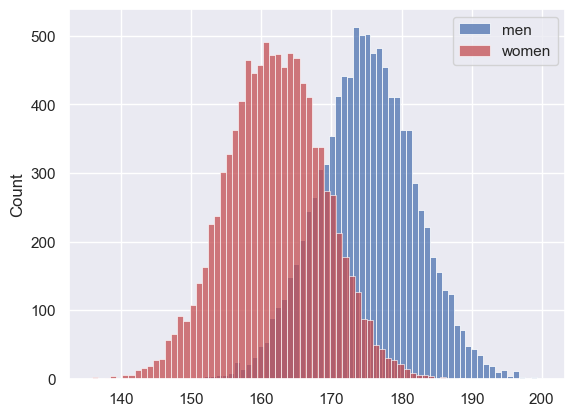
We can see that on average men are taller than women, but some women are taller than some men.

Pick a random individual

We are now going to pick a random man from our array men, using the numpy method numpy.random.choice()

# choose 1 man from the array "men", without replacement
m = np.random.choice(men, 1, replace=False)
print(m) # this is his height

[180.01482293]

Let’s also pick a random woman.

w = np.random.choice(women, 1, replace=False)
print(w) # this is his height

[155.22397658]

Is the woman taller than the man?

w>m

array([False])

… probably not, although in some cases she will be (it’s random)

Repeat lots of times

If we pick 100 man-woman pairs, in how many pairs will the woman be taller than the man?

Let’s simulate it with a for loop

woman_taller = np.empty(100) # create an empty array to store the results

for i in range(100):
    m = np.random.choice(men, 1, replace=False)
    w = np.random.choice(women, 1, replace=False)
    woman_taller[i]=w>m

woman_taller

array([0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0.,
       1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       1., 0., 0., 0., 0., 0., 0., 1., 0., 0., 1., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

Hm, what happened?

Each time we checked if the woman was taller (w>m) and put the result into a numpy array, where:

• True becomes 1
• False becomes 0

It would be handy if we could automatically count the 1s - we do this by simply adding up (or ‘summing’) all the values in the array using numpy.sum().

woman_taller = np.empty(100) # create an empty array to store the results

for i in range(100):
    m = np.random.choice(men, 1, replace=False)
    w = np.random.choice(women, 1, replace=False)
    woman_taller[i]=w>m

count = np.sum(woman_taller) # this counts how many 'True's there are in the array

print('the woman was taller ' + str(count) + '/100 times')

the woman was taller 4.0/100 times

Try running the block above a few times.

You should get a different number of pairs where the woman is taller each time you run it.

n = 5

Now we are going to do the same thing, but instead of comparing an individual man to an individual woman each time, we are going to pick 5 men and 5 women, and compare the mean heights for each group.

Also, you are going to write this one yourself!

Here are some hints:

# This code picks 1 person from the array "men" - how could you change it to pick 5?
# try it and see if it works!
m = np.random.choice(men, 1, replace=False)
print(m)

[175.02752701]

# This code gets the mean of an array "m"
m.mean()

175.0275270110625

Further exercises

Once you have your code running, you might find you don’t get many cases where the mean height of 5 women exceeds the mean height of 5 men.

• Try increasing the number of samples from 100 to 10,000
• Try varying the sample size - how does the chance of the mean height of women exceeding the mean height of men depend on the sample size?

Simulated sampling - while loop

Can you make a new simulation that counts how many samples of size 5 we need to check before we find one where the mean height of the women exceeds the mean height of the men?

You will need to refer to the exercises on simulating dice rolls with the while loop