17.4. Logistic Regression Equation

• When should we use logistic regression rather than linear regression?

Click to reveal answer

We use logistic regression (also called binary logistic regression) when we have a binary outcome variable, such as: is the person vaccinated? Does the patient smoke? Is the pregnancy test positive or negative? Did it rain yesterday? All of these questions have two possible outcomes (vaccinated or not vaccinated, smoker or non-smoker, etc.) that will be coded as 0,1 in the data.

• Why can’t we use linear regression for binary outcomes?

Click to reveal answer

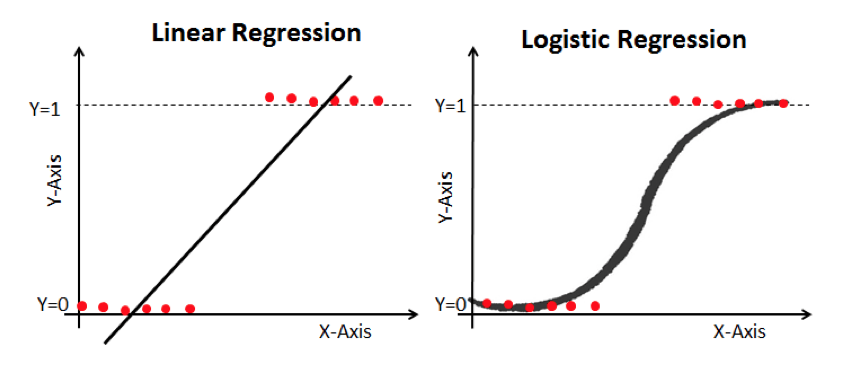
One of the assumptions of linear regression is that the observed data should contain a linear relationship, and when we have a binary outcome measure this assumption is violated. The problem is illustrated in the graph below. As the binary outcome variable can only take a value of 0 or 1 (illustrated by the red dots), the linear regression is also a problem because it is ‘unbounded’. It can take values below 0 or above 1 which would be hard to interpret in terms of predicting the probability of a yes/no outcome. In logistic regression we ‘transform’ the outcome variable so that it is bounded and can be interpreted in terms of the probability (or odds, we’ll come to this) of observing the outcome.

• What is a logit transformation?

Click to reveal answer

In logistic regression, we use the log of the odds of observing the outcome, which is called the logistic transformation, or logit for short.

The logistic equation uses the log of the odds, $\log{ \left[ \frac{p(y=1)}{1-p(y=1)} \right]} $ as the outcome

We model the logit (the log of the odds) as follows:

$$ logit(p) = \log{ \left[ \frac{p(y=1)}{1-p(y=1)} \right]} = \alpha + \beta_1 x_1 + \beta_2 x_2 + \dots \beta_k x_k $$

In a regression model with $k$ independent variables

The natural log of the odds would take a value of zero when the probability is 0.5. With a probability of 1 logit(p) would be infinity, and with a probability of 0, logit(p) would be minus infinity.

The logit transformation gets around the problem that the assumption of linearity has been violated. The transformation is a way of expressing a non-linear relationship in a linear way.

Apart from the outcome variable, the form of the regression equation is very familiar! Like in linear regression the slope estimate $\beta$ describes the change in the outcome variable for each unit of $x$, and like in linear regression, the intercept $\alpha$ is the value of the outcome variable when all $x$ variables take the value zero. However, in interpreting the coefficients, we need to keep in mind the transformation function of $y$, which we’ll practice in the next section.