1.5. Skew#

Data distributions are said to be skewed when there is a long tail of values to one side of the peak:

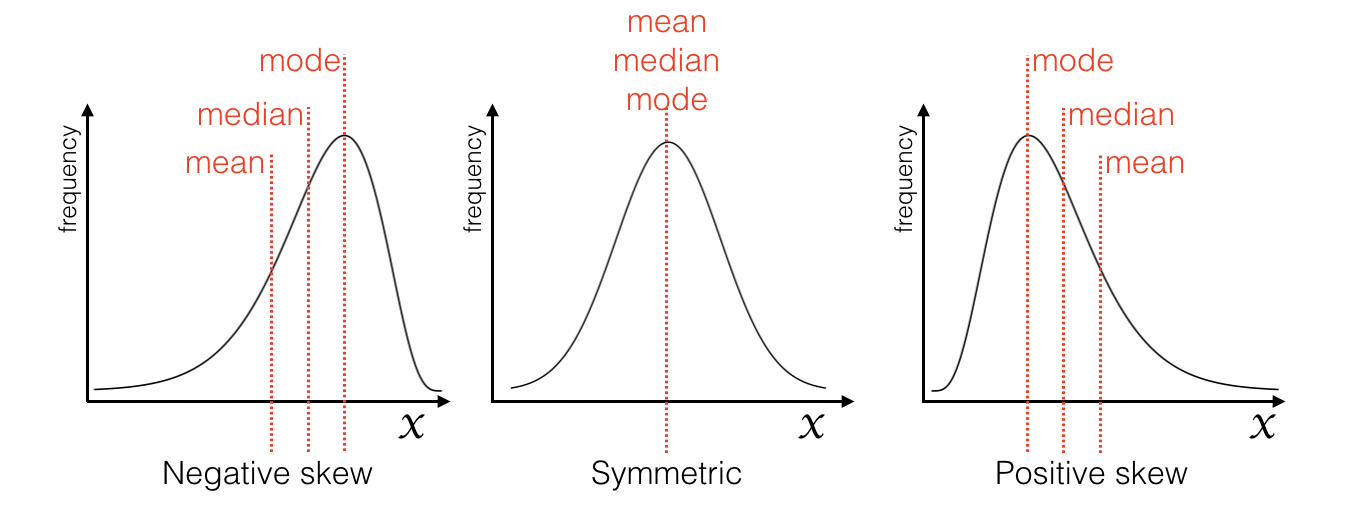
https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/images/MT_wk1_Skew.png

When a distribution is symmetrical (no skew), the mean, median and mode tend to coincide (fall on top of each other).

However, when a distribution has positive skew (a long tail of high values) the mean is dragged up above the median, and conversely when a distribution has negative skew (a long tail of low values) the mean is dragged down below the median.

To work out whether a dataset is skewed or symmetrical, we would need to plot the data (usually in a histogram). More on plotting in the next chapter.

1.5.1. Boundaries can cause skew#

Skew often arises in cases where there is a natural boundary to the range of possible data values.

For example, the distribution of income is highy positively skewed.

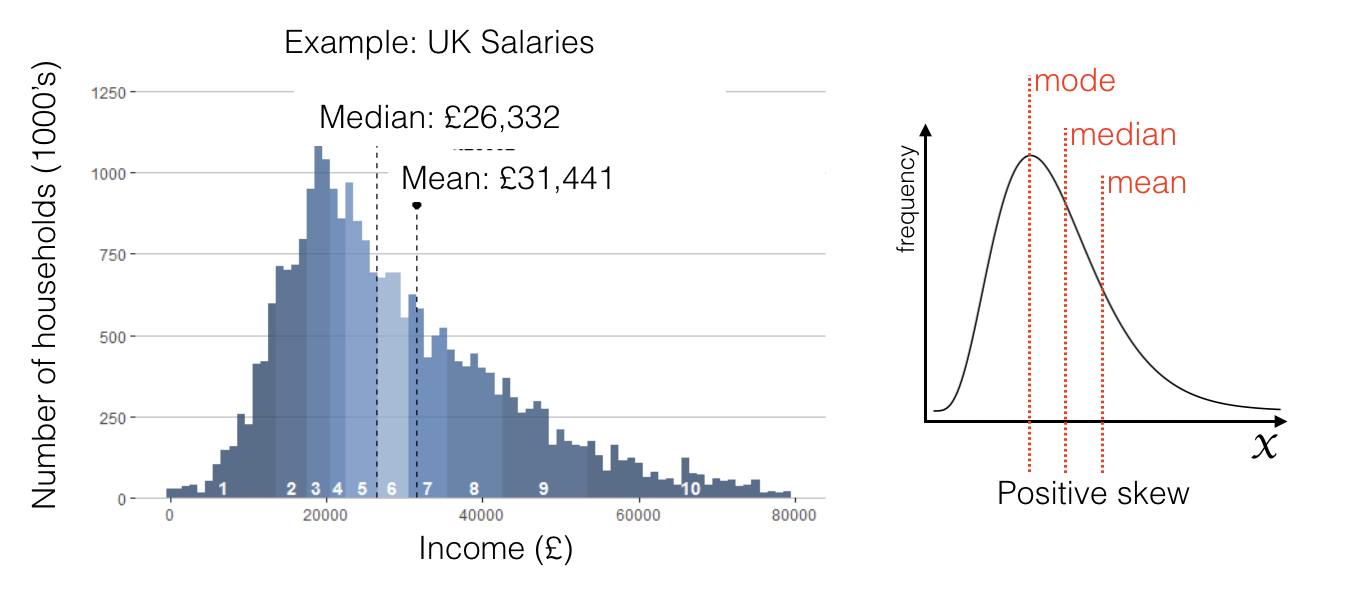
https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/images/MT_wk1_PosSkew.png

  • The median income is around £26,000.

  • Nobody’s income can be more than £26,000 below the median income (as you can’t earn less than £0)

  • However some people do earn much more than £26,000 creating a long tail of high incomes

Similarly, the distribution of age at death in modern times is negatively skewed.

.https://raw.githubusercontent.com/jillxoreilly/StatsCourseBook_2024/main/images/MT_wk1_NegSkew.png

  • the median age at death in the UK is 78

  • a lifespan could be 78 years shorter than the median (if someone sadly died as a baby)

  • a lifespan cannot be 78 years longer then the median as this would mean the person was 156 years old

Video#

Here is a video of me talking about skew and its interpretation.