2.9. Tutorial Exercises

In these exercises you will practice:

• Creating plots with Python

• Choosing appropriate plots for the question at hand

• Tweaking plots to make clear the important features of the data

• Adding comments that make the interpretation of plots clear

We will use some of the example datasets provided with Seaborn

# Set-up Python libraries - you need to run this but you don't need to change it
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pandas as pd
import seaborn as sns
sns.set_theme(style='white')
import statsmodels.api as sm
import statsmodels.formula.api as smf

2.9.1. 1. Titanic Data

The Titanic dataset contains information on 891 passengers from the Titanic.

This is actually a popular dataset for people starting out with machine learning - the task is to build a model to predict who survived (you may like to try this yourself after commpleting the session on Logistic Regression after Easter).

For now let’s use some plot to look at the factors affecting survival.

The dataset contains the following information on each passenger:

• survived 0 = No, 1 = Yes

• pclass Ticket class - 1 = 1st, 2 = 2nd, 3 = 3rd

• sex

• age Age in years

• sibsp number of siblings and/or spouses aboard the Titanic

• parch number of parents / children aboard the Titanic

• fare Passenger fare

• embarked Port of Embarkation - C = Cherbourg, Q = Queenstown, S = Southampton

• class Ticket class as a string

• who man, woman or child

• deck the deck on which they slept

• alive same as survived, but strings

• alone True only if sibsp and parch are zero

The Titanic dataset is supplied as one of the example datasets with Seaborn, so is stored on yuour computer with all the other files for Seaborn. We can load it using the special function sns.load_dataset()

# load the data - special syntax here for loading a Seaborn example dataset
titanic = sns.load_dataset('titanic')
titanic

	survived	pclass	sex	age	sibsp	parch	fare	embarked	class	who	adult_male	deck	embark_town	alive	alone
0	0	3	male	22.0	1	0	7.2500	S	Third	man	True	NaN	Southampton	no	False
1	1	1	female	38.0	1	0	71.2833	C	First	woman	False	C	Cherbourg	yes	False
2	1	3	female	26.0	0	0	7.9250	S	Third	woman	False	NaN	Southampton	yes	True
3	1	1	female	35.0	1	0	53.1000	S	First	woman	False	C	Southampton	yes	False
4	0	3	male	35.0	0	0	8.0500	S	Third	man	True	NaN	Southampton	no	True
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
886	0	2	male	27.0	0	0	13.0000	S	Second	man	True	NaN	Southampton	no	True
887	1	1	female	19.0	0	0	30.0000	S	First	woman	False	B	Southampton	yes	True
888	0	3	female	NaN	1	2	23.4500	S	Third	woman	False	NaN	Southampton	no	False
889	1	1	male	26.0	0	0	30.0000	C	First	man	True	C	Cherbourg	yes	True
890	0	3	male	32.0	0	0	7.7500	Q	Third	man	True	NaN	Queenstown	no	True

891 rows × 15 columns

Let’s first have a look at who the passengers were

a. Were there equal numbers of men and women in each class?

# Your code here

b. What was the age distribution in each class?

You could use a violin plot or a histogram here

Which is better and why?

# Your code here

c. Were people in some classes more likely to survive?

You could use countplot or barplot here.

Which is better and why?

# your code here

d. Were women and children more likely to survive?

Again you could use countplot or barplot here.

Which is better and why?

# your code here

e. Does the answer to d) depend on the ticket class?

As you are now plotting a barchart with data breoken down by two categorical variables, you will need to set one as x and one as hue.

Try it both ways and see which you think is better.

# your code here!

2.9.2. 2. Penguin data

How can we recognise penguins of different species? Let’s look at the Palmer Penguins dataset which contains data on penguins from three species (Artwork by @allison_horst):

We can see that they differ in the shape of their bills, and their size.

Let’s load the data

penguins = sns.load_dataset('penguins')
penguins

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	Male
1	Adelie	Torgersen	39.5	17.4	186.0	3800.0	Female
2	Adelie	Torgersen	40.3	18.0	195.0	3250.0	Female
3	Adelie	Torgersen	NaN	NaN	NaN	NaN	NaN
4	Adelie	Torgersen	36.7	19.3	193.0	3450.0	Female
...	...	...	...	...	...	...	...
339	Gentoo	Biscoe	NaN	NaN	NaN	NaN	NaN
340	Gentoo	Biscoe	46.8	14.3	215.0	4850.0	Female
341	Gentoo	Biscoe	50.4	15.7	222.0	5750.0	Male
342	Gentoo	Biscoe	45.2	14.8	212.0	5200.0	Female
343	Gentoo	Biscoe	49.9	16.1	213.0	5400.0	Male

344 rows × 7 columns

a. Are males bigger than females?

• Plot the mean bodyweight for each sex

• Plot the distribution of bodyweights of each sex

# your code here!

What did we learn by plotting the distribution? Can you make a further plot to explore this discovery?

# your code here!

Looks like

• All species have a similar sex difference as a proportion of their size

• Indeed one species is larger - Gentoos are the big ones

b. Is there a correlation between beak length and depth?

Plot the data in a way that answers this question.

# your code here

Do you notice some clusters in the plot? How could they be explained?

Modify your plot using the ‘hue’ argument to test your hypothesis.

Summarize your findings in plain English.

# your code here

2.9.3. 3. Parietal neurons dataset

I mentioned that Seaborn was built by a neuroscientist, Michael Waskom, and a couple of the example datasets are from neuroscience.

Here we explore the dots dataset, from a study by Roitman and Shadlen (2002). This study contains firing rates over time from neurons in the parietal cortex of a monkey performing a perceptual decision-making task.

In the task, the monkey observes a random dot kinematogram - a stimulus containing dots that mainly move about at random. A small proportion of dots move coherently upwards of downwards.

The monkey’s task is to indicate the direction in which the dots are moving - instead of pressing a button, the monkey moves its gaze to one of two targets on the screen:

• up = move eyes to target T1

• down = move gaze to target T2

The explanation for this dataset is somewhat involved (although PPL and BMS students will in fact cover this study in lectures after Christmas) but it may be helpful to see the following figure, which is what we are eventually aiming for:

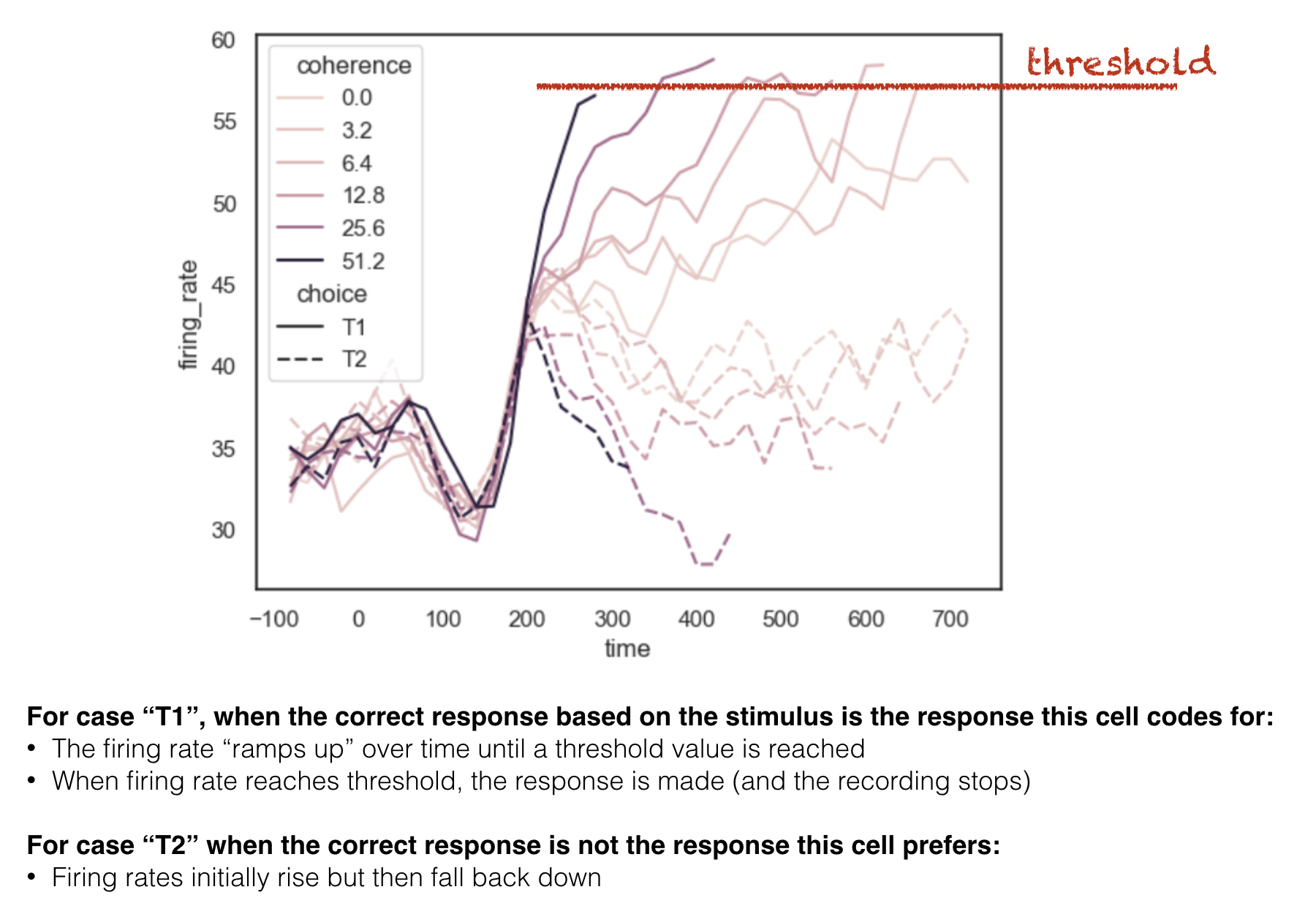
We are going to try and reproduce this figure

Let’s start by loading the data and plotting the timeseries:

dots = sns.load_dataset('dots') # this syntax only works for the Seaborn example datasets
dots

	align	choice	time	coherence	firing_rate
0	dots	T1	-80	0.0	33.189967
1	dots	T1	-80	3.2	31.691726
2	dots	T1	-80	6.4	34.279840
3	dots	T1	-80	12.8	32.631874
4	dots	T1	-80	25.6	35.060487
...	...	...	...	...	...
843	sacc	T2	300	3.2	33.281734
844	sacc	T2	300	6.4	27.583979
845	sacc	T2	300	12.8	28.511530
846	sacc	T2	300	25.6	27.009804
847	sacc	T2	300	51.2	30.959302

848 rows × 5 columns

The dataset contains timeseries alligned to two timepoints:

• stimulus onset (align == ‘dots’)

• response (saccade) onset (align == ‘sacc’)

We are going to split the dataframe and deal with these separately:

dots_stimulus = dots.query('align == "dots"')
dots_response = dots.query('align == "sacc"')

Let’s start with the stimulus-locked data.

a. Plot the timeseries data: firing rate over time

# Your code here

Time zero is the onset of the moving dots. We can see that firing rate initially dips, then rises over the course of several hundred milliseconds.

• what do your notice about the variability in firing rate?

• Could some of this variability be explained by the other variables in the dataset?

b. Separate firing rates for chosen and unchosen target

Parietal neurons are tuned to locations in space. It turns out that each neuron is more active when an eye movement is planned towards its prefered target.

This dataset is coded such that T1 is always the preferred location of the cell being recorded.

• T1 is actually a different location in space for each neuron!

On some trials T1 is chosen, and on other trials T2 (a non-preferred location) is chosen.

Let’s plot these separately using the hue argument:

# Your code here

What do you see? Describe the graph in words.

c. Effect of task difficulty

The difficulty of the task, and hence the time needed to reach a decision, depends on the proportion of coherent motion (ie what % of dots are moving to the right, or left, rather than randomly)

When only a small percentage of dots are moving coherently, the monkey needs to stare at the stimulus for a long time to work out whether the dots are moving left or right.

Let’s try breaking down the traces by level of coherence

• coherence = % dots moving left (or right) rather than randomly

You previously used hue (line colour) to break down the data by the choice (T1/T2). You can use style (different line styles) to further break down the data.

# Your code here

d. Explore use of hue and style to best represent the data

If you used hue = choice and style = coherence above, try switching these.

# Your code here

• I think this plot shows the structure in the data much more clearly than the one in part c.

• What makes it clearer?

  • which is more striking - colour (hue) or linestyle (style)

  • which more clearly conveys an ordering (from low to high coherence) - colour or line style?

e. Plot data aligned to response

The traces for T1 trials all seem to end when the firing rate reaches about 60Hz - this happens earliest for high coherence trials.

The reason the traces end is because at this point, the monkey releases an eye movement.

Now let’s plot the data aligned to the response, which we put in a separate dataframe way back at the start of this section. You can use the same plot style as in part d.

# Your code here

Focussing on trials in which choice == T1, we see:

• Aligining the data the the response brings the point at which each trace reaches threshold (60Hz firing rate) into line.

• Now we see the trace for low-coherence trials stretches further back in time than those for short coherence trials (this is the effect is also seen in the stimulus-locked plot)

f. Compare plots of stimulus- and response-locked data

Let’s use plt.subplot() to plot the stimulus and response-locked data.

• Would it be best to plot the data one above the other, or side by side? Why?

• Think about what needs to match between the axes to facilitate comparison

• Do you need to adjust the figure size to make enough space for both subplots?

# Your code here

Note-

From the stimulus-locked graph, it looks like the neurons are ramping up to a threshold.

Paired with the response-locked graph, this result is extremely convincing. This is because of the aligned peaks and the sudden drop-off of firing rate after the threshold is reached.

Aside-

You might have noticed that the threshold/peak looks higher in the response-locked graph! This looks a bit odd.

It is because the traces in the stimulus-locked graph are truncated 100ms before response onset.

• Check what the firing rate is at time -100ms in the response-locked graph (hopefully similar tho the traces’ end-points in the stimulus-locked plot)