1.7. Concepts Review#
Here we review some conceptual points from the lecture.
Please try to answer each question yourself before clicking to reveal the answer
You can discuss these points with your tutor at the computer-based tutorial session (these sessions are for discussing concepts as well as for developing Python skills)
- The fertility rate (mean number of children per adult woman) varies in Western Europe between a low of 1.3 (Italy and Spain) and a high of 1.9 (Ireland).
For each woman, the number of children is a whole number, such as 0, 1, or 2.
Does it make sense to measure a mean number of children per adult woman when the mean is not a whole number? Why or why not?
Click to reveal answer
Yes, it makes sense to report non-integer values as the mean. Obviously we wouldn’t get much information if we rounded these numbers to integers. The mean is a summary statistic not a data value, so doesn’t have to behave like a data value (i.e. data values must be integers but the mean doesn’t have to be). One property of the mean is that it tells us how many children we would expect a group of women to have – e.g. 100 Irish women would have about 190 children.
- Give an example of a variable for which the mode applies, but not
the mean or the median.
Click to reveal answer
A categorical variable, like favourite colour
- A unimodal data set has mean = 50, median = 30 and mode
= 10. Sketch and describe the data distribution
Click to reveal answer
This must be a positively skewed distribution
- The inter quartile range (IQR) is a robust measure of spread. Why
is IQR robust? What is meant by robust and why is this a desirable
quality?
Click to reveal answer
Robust means it is not strongly affected by outliers. The IQR is not affected by outliers because by definition these would lie outside the 25th-75th centile. Robustness is desirable as including outliers in a measure of spread would make the spread seem artificially large. It is especially important if you think that outliers might reflect an error in data recording, or individuals who are not reflective of the general population.
- An architect is designing a multi-story carpark. She needs to calculate the expected weight of the cars on each floor. 200 cars can park on each floor. Which measure of average car weight is more useful, the mean or the median?
Click to reveal answer
Mean, because 200 x mean would give a good estimate of what 200 cars weigh (this is NOT true for the median)
- The same architect needs to decide on the length of parking
bays. She decides to choose one length for ‘standard’ bays that will
fit most cars, and another length for ‘extra long’ bays that will fit
almost any car. What statistics does she need?
Click to reveal answer
She needs to know centiles of the distribution, say the 90th and 99th centile
- Give an example of a variable having a distribution that you expect to be
a) Approximately symmetric
b) Skewed to the right
c) Skewed to the left
d) Bimodal
e) Skewed to the right, with a mode and median of 0 but a mean greater than 0
In each case justify your choice (one short sentence)
Click to reveal answer
a) Height of men – the mean is a long way from the minimum value (zero) and there is no reason for asymmetry in the distribution b) Income – the mean is not far (not many standard deviations) above the minimum value, and there is no maximum – some people can earn many standard deviations above average but no-one can earn below zero c) Age at death – some people die young but there is a natural maximum; most people live til near this maximum d) Height of a mixed group of men and women (as men and women have different average heights) e) Number of speeding fines someone got in the last year. You can’t get less than zero, many people get zero (including all those people who can’t drive) but some people get lots.
- A teacher summarizes grades on the midterm exam as follows:
- Min 26
- Q1 67
- Median 80
- Q3 87
- Max 100
- Mean 76
- Mode 100
- Standard deviation 76
- IQR 20
Click to reveal answer
The standard deviation is incorrectly recorded. It exceeds the range of the data.
- An exam is graded on the scale 1-100 and the mean score is 76. Which value is the
more plausible for the standard deviation: -20, 0 , 10, or 50? Why?
Click to reveal answer
10 is realistic; –20 is impossible since the standard deviation cannot be negative; 0 implies that every student scored 76 on the exam, which is highly improbable; 50 is too large (it is half of the possible range of scores).
- A researcher measures weight (in stone) and height (in inches) for men. She calculates the correlation and covariance. She then decides to convert her data to metric units, kilograms and centimetres. One kilogram is 0.157 stone and one centimetre is 0.39 inches. What will happen to the correlation and covariance?
Click to reveal answer
correlation won’t change is it is normalized by s.d. in x and y and therefore unaffected by units
covariance will increase as the spread in weight and height are both greater for metric units (ie range of weights in kg is greater than range of weights in stone; range of heights in cm is greater than range of heights in inches)
- What are the assumptions of Pearson's r?
Click to reveal answer
- no outliers
- straight line relationship
- homoscedasticity
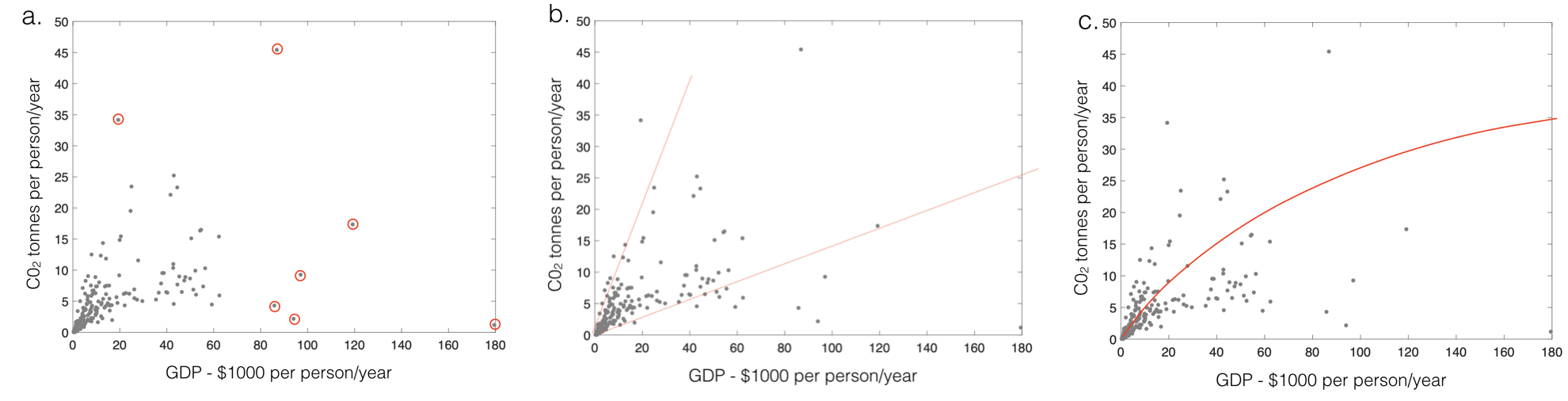
- Which features of each illustration above violate the assumptions
of Pearson's r?
Click to reveal answer
- outliers
- heteroscedasticity
- straight line relationship
- What is heteroscedasticity?
Click to reveal answer
The ice cream cone effect!
Heteroscedasticity is when the variance in y differs for different values of x (or vice versa).
- Explain why heteroscedasticity is common in real datasets
Click to reveal answer
Often the variability in data is proportional to their mean value.
For example consider a dataset of weight (y) against age (x) from birth to adulthood.
The difference between a light and heavy two year old is only a few kg (as a two year old weighs less than 20kg), but the difference between a light and heavy adult is much greater as the average weight of an adult is greater.
